".
Area of Triangles |
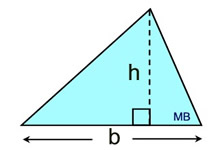 b = base and h = height to that base
b = base and h = height to that base |
Area (all triangles)
|
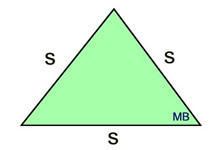 s =
side length
s =
side length |
*Area (equilateral triangle)
|
* The formula for finding the area of ANY (and ALL) triangles is A = ½bh.
It just so happens that the equilateral triangle also has a "fancy" formula to find the area if only the lengths of the sides are known. Of course, you can still use the A=½bh formula on the equilateral triangle when given the needed information.
 The formula you need to memorize for the area of triangles is A = ½ The formula you need to memorize for the area of triangles is A = ½ |
|
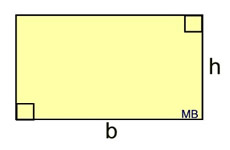 b = base and h = height
l = length and w = width may also be used
b = base and h = height
l = length and w = width may also be used |
Area (rectangle)
|
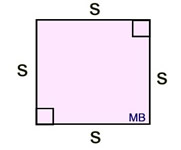 s = side length
s = side length |
Area (square)
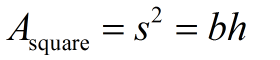
A square is a special type of rectangle, so the formula for the area of a rectangle, A = bh, will work just fine for a square.
Just remember, that in the square the b = h
|
 b = base and h = height
b = base and h = height |
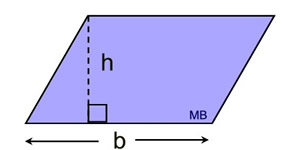
Area (parallelogram)
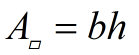
The height is drawn perpendicular to the base being used to find the area.
|
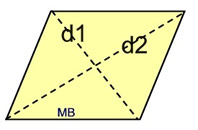 d1 = diagonal 1; d2 = diagonal 2
d1 = diagonal 1; d2 = diagonal 2 |
*Area (rhombus)
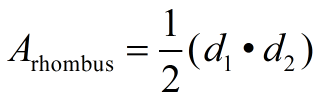
The rhombus is a special type of parallelogram, so the formula for the area of the parallelogram, A = bh, will work nicely for the rhombus as well.
|
* For the "parallelogram group", the area formula, A = bh, will work nicely for all four figures (listed above). The rhombus also has a "fancy" formula for finding the area when you know the diagonals, but the formula A = bh also works for the rhombus.
 Regarding the "parallelogram group", the formula you need to memorize Regarding the "parallelogram group", the formula you need to memorize
is A = bh, with emphasis on the rectangle and square.
When working with the parallelogram and rhombus, decomposition (cutting the shape up into triangles and rectangles) will be the preferred method, at this level, for finding area. |
Area of Trapezoid |
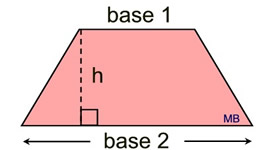
base 1 = length of one parallel side
base 2 = length of other parallel side
h = height drawn between the bases
|
*Area (trapezoid)
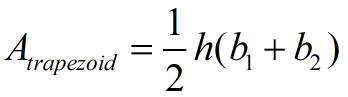
The height is drawn perpendicular to the bases being used to find the area. |
| * The definition of trapezoid: a quadrilateral with at least one pair of parallel sides. |
Area of Circle and Sectors of a Circle
(Sectors are like "pizza" pie slices of a circle.) |
|
Area (circle)
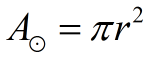 Answers may be in terms of π
Answers may be in terms of π
or a rounded decimal. |
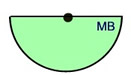 Semi-circle
Semi-circle
(half of circle = half of area)
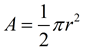
|
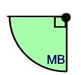 Quarter-circle
Quarter-circle
(¼ of circle = ¼ of area)
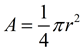
|
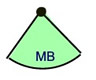 Any Sector
Any Sector
(fractional part of the area)
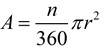 n
n = degrees in central angle of sector
|
|
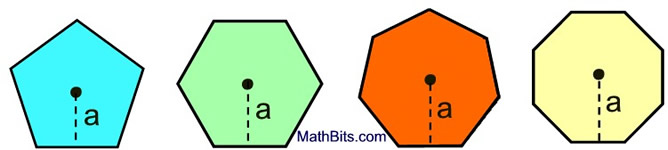
Area of Regular Polygons
|
| |
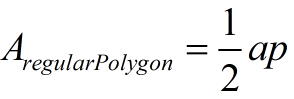 |
Regular polygons have all sides of equal length.
a = apothem
p = perimeter |
|

