|
Perimeter is the distance around the outside of a two-dimensional figure. |
|
|
To find the perimeter, add together
the lengths of all of the sides of the figure.
|
Perimeter questions may deal with given diagrams,
with geometric figures referred to by name,
or with real world problems.
Given diagram: (where all of the needed information is given)
|
Find the perimeter.
All of the information you need is given.
Add the lengths of all four sides.
18 + 9 + 18 + 9 = 54
Perimeter = 54 |
Given named geometric figure: (a figure referred to by name)
Find the perimeter of a square
with a side length of 9. |
You need to know that a square has four sides of equal length.
Then the perimeter is easy.
9 + 9 + 9 + 9 = 36
Perimeter = 36 |
Given a real world problem: (the problem describes, and/or shows the situation)
For a school art project, you need a piece of string long enough to wrap around the outer edge of this starfish. What is the shortest possible length of the string?
 |
|
For this problem, a labeled diagram is given, making the solution easier to determine.
Add all of the lengths.
2 + 1.5 + 2 + 2 + 3 + 2.5 + 2 + 2 + 1.5 + 1 = 19.5
Perimeter = 19.5 inches |
Figures referred to by their number of sides:
(see more information on types of quadrilaterals at Quadrilaterals)
| Triangle |
3 sides |
| Quadrilateral |
4 sides |
| Pentagon |
5 sides |
| Hexagon |
6 sides |
| Heptagon or Septagon |
7 sides |
| Octagon |
8 sides |
| Nonagon |
9 sides |
| Decagon |
10 sides |
| Dodecagon |
12 sides |
|
Perimeter problems may refer to shapes with a specific number of sides, by name.
Listed at the left are some of the more common polygons whose names may be used.
Remember that "regular polygons" are polygons whose sides are all the same length and whose angles are all the same size. Not all polygons are "regular". |
Certain perimeters can be expressed as "formulas".
A formula will not be needed to solve most numerical perimeter problems.
But mathematicians love formulas!
Perimeter formulas may often used to solve problems that combine algebra with geometry.
Below you will see a few examples of the expression of a formula for perimeter.
|
Triangle
perimeter = a + b + c |
|
|
Equilateral Triangle
perimeter = a + a + a = 3a |
|
 |
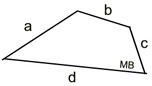Quadrilateral
perimeter = a + b + c + d |
|
 |
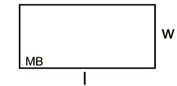Rectangle
perimeter = 2l + 2w
l = length; w = width
|
|
|
|
Regular Hexagon
perimeter = 6s |
|
