Practice Page
Directions: Read carefully!
1.
a) Explain why sin(x) = cos(90 - x) when x represents an acute angle.


b) Is it ever possible that sin(x) = cos(x)? Explain your answer.


 

 

2.
In right ΔABC, m∠C = 90º, if sin A = m, find cos B.

Choose:
90 - m
45 - m
90 + m
m

 

 

3.
Solve for θ (angles are acute):
a) cos 60º = sin θ
Choose:
30º
45º
60º
90º

b) sin 71º = cos θ
Choose:
71º
35º
29º
19º
 
 

c) sin θ = cos (θ + 20)
Choose:
20º
35º
60º
70º
 

d) sin (θ - 60) = cos θ
Choose:
75º
35º
30º
15º

 

 

4.
Given right triangle ABC with right angle C, and sin A = ¼. Which of the following expressions are also equal to ¼?
Select all that apply and hit "Submit".

1. cos(A)

2. cos(B)

3. cos(90º - A)

4. cos(90º - B)

5. sin(B)

 

 

5.
In attempting to solve for x in the problem at the right, students responded with a variety of equations. Which, if any, of the following equations are correct?
Select all that apply and hit "Submit".

1. scprac1

2. scprac2

3. scprac3

4. scprac4

5. scprac5

6. None are true.
sctriangle

 

 

6.
In right ΔABC, m∠C = 90º, cos A = 1/5.
What is sin B ?

Choose:
1/5
3/5
90 - 1/5
90 - 4/5

 

 

7.
In right ΔABC, m∠C = 90º. Simplify the following expression: 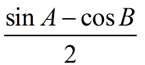scg
 
Choose:
30
45
90
0

 

 

8.
Given that sin (x + 10)º = cos (3x + 20)º, find the number of degrees in the acute angles of the corresponding right triangle.

Choose:
30º and 60º
45º and 45º
25º and 65º
40º and 50º

 

 

9.
In right ΔABC, m∠C = 90º, sin A = 3x - 0.6 and cos B = 4x - 0.9.
Find x.

 
Choose:
0.3
0.4
0.6
1.5

 

 

10.
In right ΔABC, m∠C = 90º and m∠A does not equal the m∠B.
If sin A = m and cos A = k, find cos B + sin B.           

Choose:
m + k
m - k
k - m
90 - (m + k)

 

 

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".