|
Directions: Read carefully.
1. |
a) How many lines of symmetry does a square possess?
Choose:
b) What is the minimum angle of rotation about the center that will carry a square onto itself?
Choose:
|
|
|
2. |
a) The figure at the right has one, and only one, line of symmetry.
Choose:
|
 |
| |
b) Which quadrilateral has one, and only one, line of symmetry?
Choose:
|
|
3. |
a) The figure at the right has no line symmetry, but has rotational symmetry of 180º.
Choose:
|
 |
b) Which quadrilateral has no line symmetry, but has rotational symmetry of 180º (Order 2)?
Choose:
|
|
4. |
a) Which of the following figures has a minimum rotational symmetry of 120º (Order 3)?
Choose:
|
b) What is the other angle between 0º and 360º of rotational symmetry of the object described in part a?
Choose:
|
|
5. |
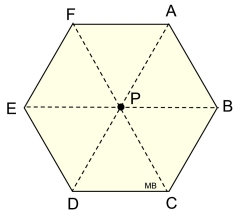
a) In a regular hexagon, what is the angle of rotation?
Choose:
b) In a regular hexagon, how many angles between 0º and 360º will carry the polygon onto itself?
Choose:
|
 |
| |
c) What counterclockwise angle of rotation about point P will carry point F onto point D?
Choose:
|
|
6. |
The car wheel shown at the right has both line and rotational symmetry.
a) State the number of lines of symmetry. Choose:
b) State the degree measure of the angle of rotation.
Choose:
|
|
|
7. |
A segment equal in length to the radius of a circle is repeated around the circle, forming chords from end to end. Two repetitions of the segment are shown at the right.
a) How many segments will be able to be placed in this manner around the circle?
Choose:
|
|
|
b) What will be the angle of rotation of the figure formed by the repetition of the segment?
Choose:
|
|
8. |
ΔABC is an isosceles triangle with
AC = BC.
What is the equation of the line of symmetry of this triangle?
Choose:
|
|
|
9. |
ABCD is a square. The grid pattern in the interior of the square forms a series of small squares.
a) How many lines of symmetry will ABCD possess, including the internal grid pattern?
|
|
|
|
10. |
ΔABC is an equilateral triangle. The triangles in the interior of ΔABC are also equilateral triangles.
Which of the following statements is true regarding this entire diagram?
|
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|