To review the basic concepts of symmetry, see the section Transformations - Symmetry.
On this page, we will expand upon those review concepts of line symmetry,
point symmetry, and rotational symmetry, from a more geometrical viewpoint.
When working with transformations, the "symmetry of an object" is described as
a rigid transformation that moves an object back onto itself.
There are two types of such symmetries: reflectional symmetry and rotational symmetry.

Reflectional Symmetry or Line Symmetry |
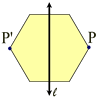
Basically, a line of symmetry is a line that divides a figure through its center
into two mirror images.
The figure is mapped onto itself by a reflection in this line.
|
A set of points has line symmetry if and only if there is a line, l, such that the reflection through l of each point in the set is also a point in the set. (May also be referred to as reflectional symmetry.) |
|
|
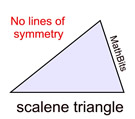
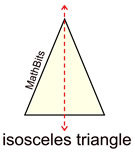
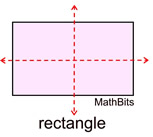
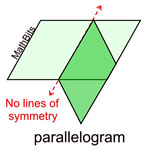
Certain figures can be mapped onto themselves by a reflection in their lines of symmetry. Some figures have one or more lines of symmetry, while other figures have no lines of symmetry.
(Remember, if you fold the figure on a line of symmetry, the folded sides coincide.)
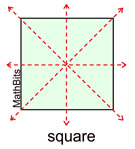
Lines of Symmetry:

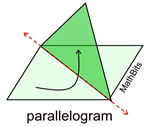
Not all lines that divide a figure into two congruent halves are lines of symmetry.
Some special circumstances:
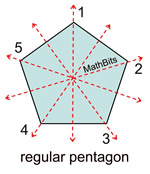
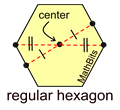
In regular polygons (where all sides are congruent and all angles are congruent), the number of lines of symmetry equals the number of sides.
(Start by drawing the lines through the vertices.) |
|
|
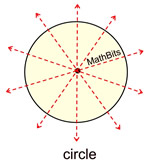
When working with a circle, any line through the center of the circle is a line of symmetry.
There are an infinite number of lines of symmetry. |
|
|
 In regular polygons, the number of lines of symmetry
In regular polygons, the number of lines of symmetry
equals the number of sides in the polygon.

Reflectional Symmetry or Point Symmetry |
Basically, a figure has
point symmetry when it looks the same when up-side-down,
(rotated 180º), as it does right-side-up.
|
A figure has point symmetry if it is built around a point, called the center, such that for every point |
|
on the figure there is another point directly opposite and at the same distance from the center.
Point symmetry can also be described as rotational symmetry of 180º. |
|
Examples of geometric figures in relation to point symmetry:
Point Symmetry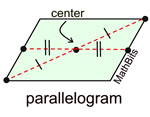 |
Point Symmetry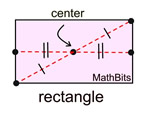 |
No Point Symmetry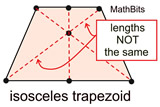 |
No Point Symmetry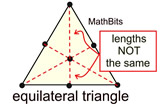 |

Basically, a figure has rotational symmetry if when rotating (turning or spinning) the figure around a center point by less than 360º, the figure appears unchanged. The point around which the figure is rotated is called the center of rotation, and the smallest angle needed for the "spin" is called the angle of rotation.
|
A geometric figure has rotational symmetry if the figure appears unchanged after a |
|
| rotation about a point by an angle whose measure is strictly between 0º and 360º. The angles of 0º and 360º are excluded since they represent the original position (nothing new happens). The angles of rotational symmetry will be factors of 360. |
|
The number of positions in which the rotated object appears unchanged is called the
order of the symmetry. Order 2 implies an unchanged image at a rotation of 180º (splitting 360º into 2 equal parts). Order 3 implies an unchanged image at 120º and 240º (splitting 360º into 3 equal parts), and so on. Order 1 implies no true rotational symmetry exists, since a full 360 degree rotation is needed to again display the object with its original appearance.
There is a relationship between the angle of rotation and the order of the symmetry.
Examples of geometric figures and rotational symmetry:
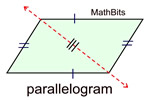
Spin this parallelogram about the center point 180º and it will appear unchanged.
Order 2.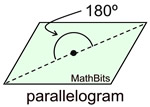 The only angle between
The only angle between
0º and 360º that will carry the figure onto itself is 180º. |
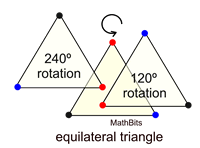
Spin this equilateral triangle on the center point and every 120º it will appear unchanged.
Order 3.
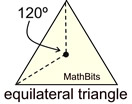 The only angles between
The only angles between
0º and 360º that will carry the figure onto itself are
120º and 240º.
|
Spin this square about the center point and every 90º it will appear unchanged.
Order 4.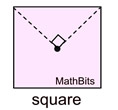 The only angles between
The only angles between
0º and 360º that will carry the figure onto itself are
90º, 180º, and 270º. |
Spin a regular pentagon on its center point and every 72º it will appear unchanged.
Order 5. 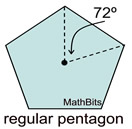 The only angles between
The only angles between
0º and 360º that will carry the figure onto itself are
72º, 144º, 216º, and 288º. |
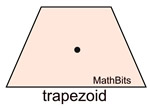
Not all figures have rotational symmetry. A trapezoid, for example, when spun about its center point, will not return to its original appearance until it has been spun 360º. It has no rotational symmetry. Order 1.
Remember that Order 1 really means NO rotational symmetry.
|
 |
|