|
Let's look at some special situations involving combinations:
 In certain cases, a combination of transformations may be renamed by a single transformation. In certain cases, a combination of transformations may be renamed by a single transformation. |
Example: 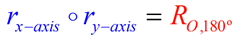
The combination of a line reflection in the y-axis, followed by a line reflection in the x-axis, can be renamed as a single transformation of a rotation of 180º in the origin (also called a reflection in the origin).
It is not possible to rename all compositions of transformations with one transformation, however:
|
|
Any translation or rotation can be expressed as the composition of two reflections. |

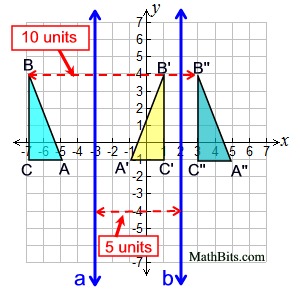
 A composition of reflections over two parallel lines is equivalent to a translation. A composition of reflections over two parallel lines is equivalent to a translation.
(May also be over any even number of parallel lines.) |
Example: Given a || b, and pre-image ΔABC, where parallel lines are vertical. 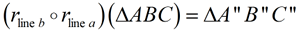
Look carefully in this situation to see which of the parallel lines will be the first line of reflection. Do not assume the parallel line nearest the pre-image (as in this example) will always be used first. |
|
It can be seen from the diagram, that Δ A''B''C'' could also be a horizontal translation of Δ ABC. The horizontal distance of the translation will be twice the width between the vertical parallel lines. 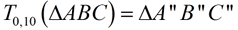
The parallel lines may be vertical (as seen in this example), horizontal or slanted.
|

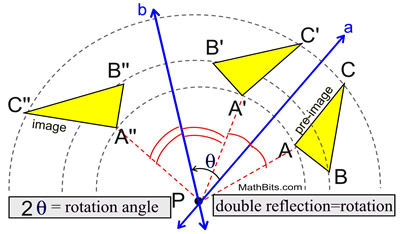
 The composition of reflections over two intersecting lines is equivalent to a rotation. The composition of reflections over two intersecting lines is equivalent to a rotation.
The center of rotation is the intersection point of the lines.
|
Example: Given two lines, a and b, intersecting at point P, and pre-image ΔABC. 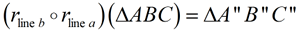 |
|
The double reflections are equivalent to a rotation of the pre-image about point P of an angle of rotation which is twice the angle formed between the intersecting lines (theta).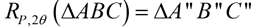
Remember that, by convention, the angles are read in a counterclockwise direction. You may also apply this rule to negative angles (clockwise).
|

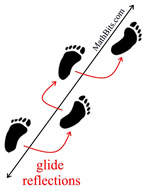
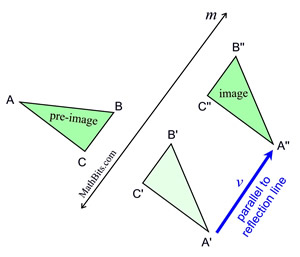
 A glide reflection is the composition of a reflection and a translation, where the line of reflection, m, is parallel to the directional vector line, v, of the translation. A glide reflection is the composition of a reflection and a translation, where the line of reflection, m, is parallel to the directional vector line, v, of the translation. |
Example: 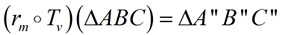
A glide reflection is commutative. Reversing the direction of the composition will not affect the outcome.
|
 |
|
Footprints are an example of several glide reflections. In the diagram at the left, you are seeing the original "step" on the left foot, followed by the "step" on the right foot, which is the "result" of the glide reflection. When compared to the diagram of the triangles, shown above, you are not seeing ΔA'B'C' (reflection) in the footprints. |

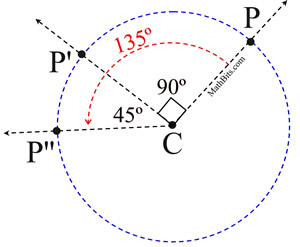
 The composition of two rotations from the same center, is a rotation whose degree of rotation equals the sum of the degree rotations of the two initial rotations. The composition of two rotations from the same center, is a rotation whose degree of rotation equals the sum of the degree rotations of the two initial rotations. |
Example: 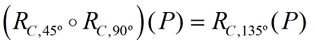
Note that CP = CP' = CP'', as they are radii of circle C. |
 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|