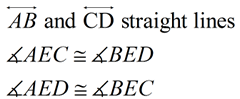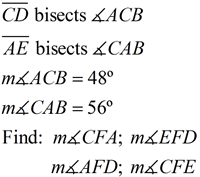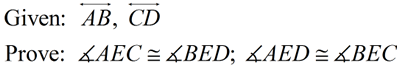|
In depth investigation of vertical angles.
|
Vertical angles are a pair of non-adjacent angles formed by the intersection of two straight line. |
|
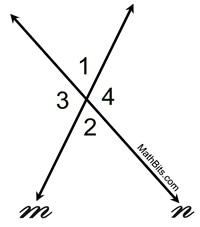
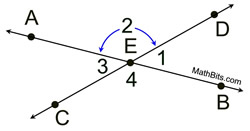
Vertical angles are located across from one another in the corners of the "X" formed by two straight lines.
In the diagram at the right, lines m and n are straight:
∠1 and ∠2 are vertical angles.
∠3 and ∠4 are vertical angles.
∠1 and ∠3 are NOT vertical angles. |
|
 |
"Vertical Angle Theorem": Vertical angles are congruent. |
|
1. 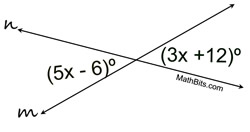 |
Given:
straight lines m and n
Find the number of degrees
in the indicated angles. |
ANSWER:
The indicated angles are vertical angles.
5x - 6 = 3x + 12
2x = 18
x = 9
5(9) - 6 = 39º
3(9) + 12 = 39º
|
2. 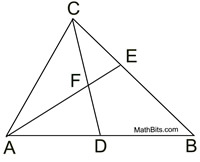 |
Given:
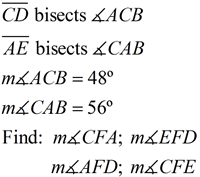
|
ANSWER:
m∠ACF=24º
m∠CAF=28º
m∠CAF=128º
m∠EFD=128º
m∠AFD=52º
m∠CFE=52º
|
3. 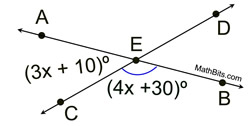 |
Given:
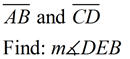 |
ANSWER:
The indicated angles are supplementary.
3x + 10 + 4x + 30 = 180
7x + 40 = 180
7x = 140
x = 20
m∠AEC=70º
m∠DEB=70º since it is vertical to ∠AEC. |

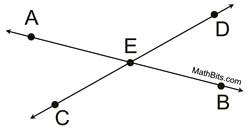
Proof of Vertical Angle Theorem - Using Transformations |
The basis for this transformational proof will be a rotation of 180º about E.
Proof:
• A rotation of 180º about point E will map point A onto 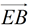 such that A will lie on such that A will lie on 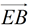 since we are dealing with straight segments. It will also map point C onto since we are dealing with straight segments. It will also map point C onto 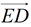 such that C will lie on such that C will lie on 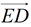 . .
• The rotation will create ∠A'EC', which will be congruent to ∠BED since they are the same angles with the same sides (rays) and same vertex.
• Since ∠A'EC' is a 180º rotation of ∠AEC about E, ∠A'EC' 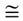 ∠AEC since rotations are rigid transformations which preserve angle measure. ∠AEC since rotations are rigid transformations which preserve angle measure.
•
∠AEC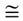 ∠BED by the transitive property of congruence (or substitution). ∠BED by the transitive property of congruence (or substitution).
• The same argument will apply to proving ∠AED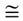 ∠BEC. ∠BEC.
Proof of Vertical Angle Theorem - Using Linear Pairs |
For this proof, we will look at the linear pair relationships between adjacent angles about point E.
Statements |
Reasons |
1. 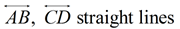 |
1. Given |
2. ∠1, ∠2 form linear pair
∠3, ∠4 form linear pair
∠1, ∠4 form linear pair
|
2. A linear pair is a pair of adjacent angles that form a straight line. |
3. ∠1, ∠2 are supplementary
∠3, ∠4 are supplementary
∠1, ∠4 are supplementary |
3. Angles that form a linear pair are supplementary. |
4. m∠1 + m∠2 = 180
m∠3 + m∠4 = 180
m∠1 + m∠4 = 180 |
4. Supplementary angles are two angles the sum of whose measures is 180º. |
5. m∠1 + m∠2 = m∠1 + m∠4
m∠1 + m∠4 = m∠3 + m∠4 |
5. Quantities equal to the same quantity are equal to each other. (Substitution or Transitive) |
6. m∠1 = m∠1; m∠4 = m∠4 |
6. Reflexive property (quantity = itself). |
7. m∠2 = m∠4; m∠3 = m∠1 |
7. If equals are subtracted from equals, the differences are equal. |
8. 
or 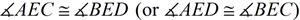
|
8. Congruent angles are angles of equal measure. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|