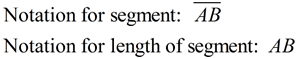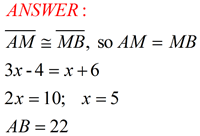Segments MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

A segment (or line segment) is a part of a line that is bounded by two distinct end points. It contains every point on the line between its end points.

Postulate:  A line segment is the shortest distacnce between two distinct points.

Ruler Postulate: The points on a line can be put into a one-to-one correspondence (paired) with the real numbers. The distance between any two points is represented by the absolute value of the difference between the numbers. [Keep in mind that distances are always positive.]

The distance between D and F is | 0 - 2 | = 2. The distance between C and E is | -2 - 1 | = 3. The distance between A and C is | -3 - (-2) | = 1.

For constructions relating to copy a segment, go to Construct: Copy a Line Segment.

Statement: If B lies on the segment from A to C, then AB + BC = AC.
Also the converse: If AB + BC = AC, then B lies on the segment from A to C.

      AB + BC = AC
Note: We are referring to "lenghts of sections" being added (i.e. AB), not physical sections themselves (i.e. ).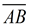

You may see examples where the concept of this postulate is referred to as "Whole quantity", "the Whole is equal to the sum of its parts" or "Betweenness of points". Be sure to use the statement that your teacher wishes to follow.

In this postulate, points A, B and C are collinear, meaning they all lie on the same line.
Point B is between points A and C on the segment.

The midpoint of a segment is a unique point on the segment forming two congruent segments.

Example:

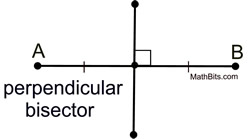
The bisector of a segment is a line, ray, or segment which cuts the given segment into two congruent segments. The point where the bisector crosses the segment is the midpoint of the segment.

There are an infinite number of possible bisectors of a segment passing through the midpoint.

Note: You may see this defintion say "two segments of equal measure" instead of "two congruent segments."
Or, it may say "cuts the segment at its midpoint". It depends on the textbook you are using.

If the bisector is also perpendicular to the segment, it is referred to as the perpendicular bisector of the segment. While there are an infinite number of possible bisectors of a segment, there is only one perpendicular bisector.

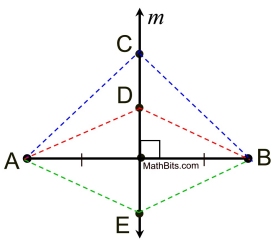
The points on a perpendicular bisector of a line segment are equidistant from the endpoints of the line segment.

In the diagram, line m is the perpendicular bisector of the segment from A to B. Every point on line m is the same distance from A, as it is from B. Distances:   AC = CB       AD = DB       AE = EB

For constructions relating to bisect segments, go to Construct: Bisect Segments (Perpendicular Bisector).