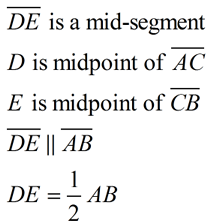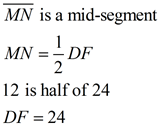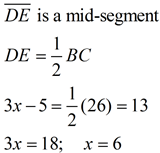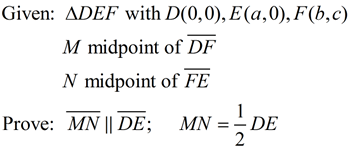|
|
The mid-segment of a triangle (also called a midline) is a segment joining the midpoints of two sides of a triangle. |
|
 |
"Mid-Segment Theorem": The mid-segment of a triangle, which joins the midpoints of two sides of a triangle, is parallel to the third side of the triangle and half the length of that third side of the triangle. |
|

1. 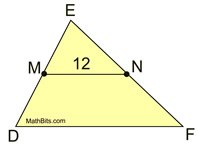 |
Given M, N midpoints.
MN = 12
Find DF. |
ANSWER:
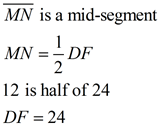
|
2. 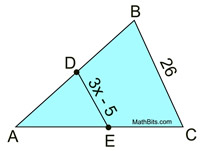 |
Given D, E midpoints.
DE = 3x - 5
AB = 26
Find x. |
ANSWER:
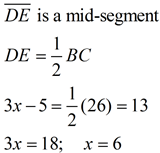
|
3. 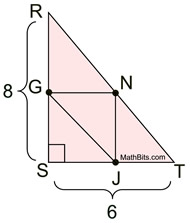 |
Given right ΔRST.
G, N, J midpoints.
ST = 6; RS = 8
Find perimeter of
ΔGNJ.
|
ANSWER:  |

Proof of Mid-Segment Theorem - Using Coordinate Geometry |
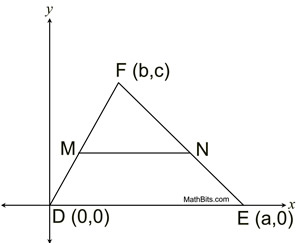
For this proof, the diagram has been positioned in the first quadrant with one side on the x-axis to keep the algebraic computations as simple as possible, without losing the general positioning of the triangle. Be aware that other positionings are also possible.
Coordinate Geometry formulas needed for this proof: |
Midpoint Formula: 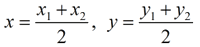 |
Distance Formula: 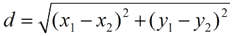 |
Proof:

Proof of Mid-Segment Theorem - Using Similar Triangles |
For this proof, we will prove ΔMFN is similar ΔDFE, by SAS for similar triangles, to obtain corresponding angles for parallel lines and establish a pair of proportional sides.
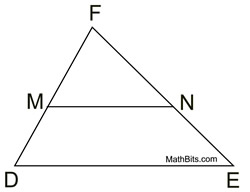 |
|
Statements |
Reasons |
1. 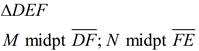 |
1. Given |
2. 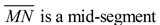 |
2. A mid-segment joins the midpoints of two sides of a triangle. |
3. 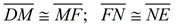 |
3. Midpoint of a segment divides a segment into 2 congruent segments. |
4. DM = MF; FN = NE |
4. Congruent segments are segments of = length. |
5. DM + MF = DF; FN + NE = FE |
5. Segment Addition Postulate (or Whole Quantity) |
6. MF + MF = DF; FN + FN = FE |
6. Substitution |
7. 2MF = DF; 2FN = FE |
7. Addition (or Combine Like Terms) |
8. 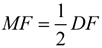 ; ; 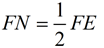 |
8. Multiplication (or Division) property of equality.
[This step establishes the ratio of similitude between the two triangles.] |
9. 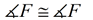 |
9. Reflexive Property (or Identity Property) |
10. 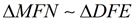 |
10. SAS for Similar Triangles: If an ∠ of one Δ is congruent to the corresponding ∠ of another Δ and the lengths of the sides including these ∠s are in proportion, the Δs are similar. |
11. 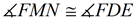 |
11. Corresponding angles in similar triangles are congruent. |
12. 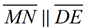 |
12. If 2 lines are cut by a transversal such that the corresponding angles are congruent, the lines are parallel. |
13. 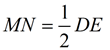 |
13. Corresponding sides of similar triangles are in proportion. QED. |
Proof of Mid-Segment Theorem - Using Parallelogram |
For this proof, we will utilize an auxiliary line, congruent triangles and the properties of a parallelogram.
Statements |
Reasons |
1. 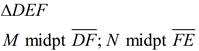 |
1. Given |
2. 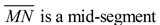 |
2. A mid-segment joins the midpoints of two sides of a triangle. |
3. Through E draw line parallel to  . Extend  to intersect at M1. |
3. Through a point not on a line, only one line can be drawn parallel to the given line. Parallel Postulate. |
4. 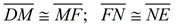 |
4. Midpoint of a segment divides a segment into 2 congruent segments. |
5. ∠ DFE 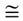 ∠ FEM1 |
5. If 2 parallel lines are cut by a transversal, the alternate interior angles are congruent. |
6. ∠ FNM 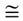 ∠M1NE ∠M1NE |
6. Vertical angles are congruent. |
7. Δ FNM 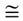 Δ M1NE |
7. ASA - If 2∠s and the included side of one Δ are congruent to the corresponding parts of another Δ, the Δs are congruent. |
8. 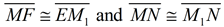 |
8. CPCTC - corresponding parts of congruent triangles are congruent. |
9. 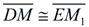 |
9. Substitution (or Transitive property) |
10. DMM1E is a parallelogram |
10. A quadrilateral with one pair of sides both || and congruent is a parallelogram. |
11. 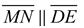 |
11. A parallelogram is a quad. with 2 pair of opposite sides parallel. |
12. 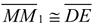 |
12. Opposite sides of a parallelogram are congruent. |
13. 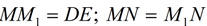 |
13. Congruent segments have = measure. |
14. MN + M1N = MM1 |
14. Segment Addition Postulate (or whole quantity) |
15. MN + MN = DE |
15. Substitution |
16. 2MN = DE |
16. Addition (or combine like terms) |
17. MN = ½DE |
17. Division (or Multiplication) of Equalities |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|