|
You have worked with "pairs" of angles in past courses.
Let's refresh and enhance some basic facts we know about these pairs.
There are some special relationships between "pairs" of angles.
 Adjacent Angles are two angles that share a common vertex, a common side, and no common interior points. (They share a vertex and side, but do not overlap.)
|
|
∠1 and ∠2 are adjacent angles.
∠ABC and ∠1 are NOT adjacent angles.
(∠ABC overlaps ∠1.) |
A Linear Pair is two adjacent angles whose non-common sides form opposite rays (a straight line). |
|
∠1 and ∠2 form a linear pair.
The line through points A, B and C is a straight line.
∠1 and ∠2 are supplementary.
|
|
If two angles form a linear pair, the angles are supplementary.
A linear pair forms a straight angle which contains 180º, so you have 2 angles whose measures add to 180, which means they are supplementary. |
|
|
If two congruent angles form a linear pair, the angles are right angles.
If two congruent angles add to 180º, each angle contains 90º, forming right angles. |
|
|
Vertical Angles are two angles whose sides form two pairs of opposite rays (straight lines). |
|
Vertical angles are located across from one another in the corners of the "X" formed by the two straight lines.
∠1 and ∠2 are vertical angles.
∠3 and ∠4 are vertical angles.
Vertical angles are not adjacent.
∠1 and ∠3 are not vertical angles (they are a linear pair).
Vertical angles are always equal in measure. |
|
Vertical angles are congruent.
Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving
m∠1 + m∠4 = 180 and m∠2 + m∠4 = 180. With substitution, m∠1 = m∠2 and they are congruent. |
|
|
Complementary Angles are two angles the sum of whose measures is 90º. |
|
Complementary angles can be placed so they form perpendicular lines, or they may be two separate angles.
∠1 and ∠2 are complementary.
∠P and ∠Q are complementary.
|
|
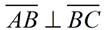
Complements of the same angle, or congruent angles, are congruent.
If m∠a is complementary to the m∠b, and m∠c is complementary to m∠b, then
m∠a = m∠c. Consider m∠a = 60º, m∠b = 30º and m∠c = 60º. |
|
|
The acute angles of a right triangle are complementary.
The sum of the angles in a triangle add to 180º. After subtracting 90º for the right angle, there are 90º left for the two acute angles, making them complementary. |
|
|
Supplementary Angles are two angles the sum of whose measures is 180º. |
|
Supplementary angles can be placed so they form a linear pair (straight line), or they may be two separate angles.
∠1 and ∠2 are supplementary.
∠P and ∠Q are supplementary.
The line through points A, B and C is a straight line. |
|
Supplements of the same angle, or congruent angles, are congruent.
If m∠a is supplementary to the m∠b, and m∠c is supplementary to m∠b, then
m∠a = m∠c. Consider m∠a = 60º, m∠b = 120º and m∠c = 60º. |
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
