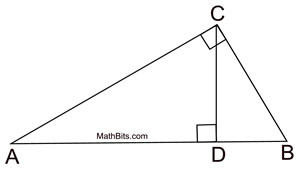
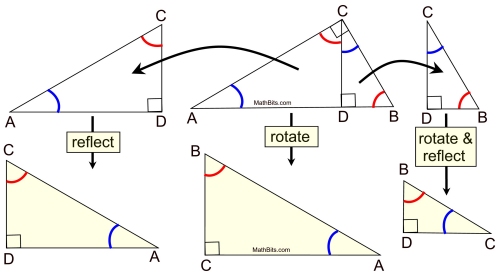
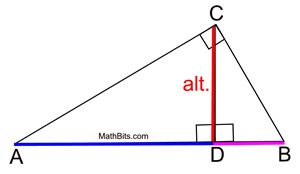
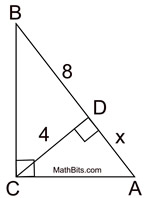
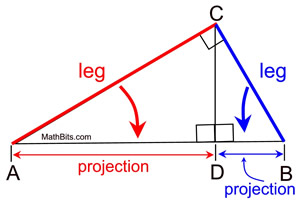
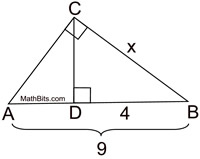
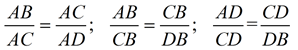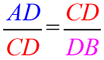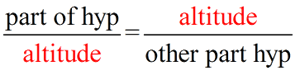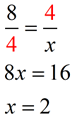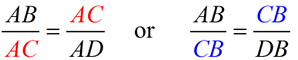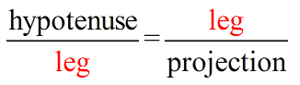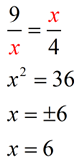Mean Proportionals in Right Triangles

Mean Proportionals in Right Triangles
Notebook

Topical Outline | Geometry Outline | Math-bits' Teacher Resources

Terms of Use Contact Person: Donna Roberts

Mean proportionals (or geometric means) appear in two popular theorems regarding right triangles. Before we state these theorems, let's take a look at a theorem relating to the triangles we will be using:

The altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle.

Let's separate the diagram, and move the sections around
so we can more clearly see the similar triangles involved.
meanth22

• ΔACB∼ΔADC by AA (Angle Angle Postulate) - each Δ has a right angle and share ∠A.
• ΔACB∼ΔCDB by AA (Angle Angle Postulate) - each Δ has a right angle and share ∠B.
• We can establish that ∠B ∠ACD because they are each complementary to ∠DCB.
ΔADC∼ΔCDB by AA - each Δ has a right angle and ∠B ∠ACD.

Since these triangles are similar, we can establish a series of proportions relating their corresponding sides. Two valuable theorems are formed using 3 of these proportions: proportions3

Remember the "look" of the given diagram for this theorem. If you "forget" the rules stated in the following theorems, you can simply recall this original diagram and set up the corresponding sides of the three similar triangles.

The altitude to the hypotenuse of a right triangle is the mean proportional between the segments into which it divides the hypotenuse.

Altitude Rule:
altrule2

Notice the triangle used with this rule! It is the same diagram used in the first theorem on this page - a right triangle with an altitude drawn to its hypotenuse.

Find x.

Solution:
Examine the diagram to see what information is given. In this problem, the "legs" are NOT labeled, but the "altitude" is labeled.

This is the "altitude rule".

The leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse.

The "projection" of a leg is that segment of the hypotenuse which is attached to (adjacent to) the leg.
A projection is formed by dropping a perpendicular from the end of the segment (leg) to the hypotenuse.
Think of a projection as a "shadow" --

is the ground with the sun directly overhead and the shadow of

meanleg
legs

Leg Rule: legrule2

Notice the triangle used with this rule! It is the same diagram used in the first theorem on this page - a right triangle with an altitude drawn to its hypotenuse. (Also same diagram as the Altitude Rule.)

Find x.

Solution:
Look carefully at the diagram.
In this problem, the "altitude" is NOT labeled, but a "leg" is labeled.

This is the "leg rule".

The length of the side of a triangle is a positive value.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use".

Topical Outline | Geometry Outline | Notebook | Math-bits' Teacher Resources
Terms of Use Contact Person: Donna Roberts