|
The following problems will demonstrate strategies and hints for
solving numerical and algebraic problems dealing with quadrilaterals.
| 1. |
 |
Given: m∠A = 3x+9 m∠B = 5x+20
m∠C = 3x m∠D = 2x+6
Find m∠D.
Solution: 3x+9 + 5x+20 + 3x + 2x+6 = 360
13x + 35 = 360; 13x = 325; x = 25
m∠D = 2(25)+6 = 56º |
| |
Remember:
•
All four sided figures (regardless of their shapes) have angles whose measures add to 360º.
• Read carefully for what is needed as an answer. This question asks for the angle measure, not for just the value of x. |
|
| 2. |
|
Given: square ABCD with a perimeter of 48 units.
Find the number of units in BD (in simplest radical form).
Solution: Each side of the square must be 12 units.
12² + 12² = (BD)²; 144 + 144 = (BD)²;
BD = 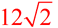 units units
|
| |
Remember:
•
Use your previous knowledge regarding geometric figures, such as perimeter being the distance around the outside of the figure.
• Always be on the look out for possible applications of your old friend, Pythagorean Theorem (especially in situations involving right angles). |
|
| 3. |
|
Given: parallelogram ABCD, sides as marked.
Find AD.
Solution: 6x - 10 = 3x + 5 (opposite sides)
3x - 10 = 5; 3x = 15; x = 5
AD = 4x - 5 = 4(5) - 5 = 15 |
| |
Remember:
•
This is where the properties of a parallelogram are needed. You know the opposite sides of a parallelogram are congruent, so set the opposite sides equal to one another.
• Be sure to pair up the opposite sides correctly. The side labeled 4x - 5 will not be used when solving for x, but will be used to solve for AD. |
|
| 4. |
|
Given: rectangle MATH, diagonals = 36 in.
Find x and y.
Solution:
Each diagonal segment = 18.
2x + 4y = 18 and 4x - y = 18
Solve simultaneously.
x = 5 (as shown at the right)
2x + 4y = 18
2(5) + 4y = 18
4y = 8
y = 2 |
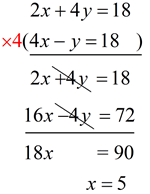 |
|
| |
Remember:
•
The properties of rectangles state that the diagonals bisect each other and are congruent. Thus the four segment lengths (ME, ET, HE, AE) are equal to 18 inches each.
• When you see two variables in a problem, consider using simultaneous equations to arrive at the solution. |
|
| 5. |
|
Given: parallelogram DEFG, ∠s as marked.
Find m∠F.
Solution:∠D supplementary to ∠E
(2x+12) + (5x) = 180
7x + 12 = 180; 7x = 168; x = 24
m∠F = 2(24) + 12 = 60º |
| |
Remember:
•
This problem is based upon the property of a parallelogram that states the consecutive angles are supplementary. If you forget this property, remember that a parallelogram has parallel lines, which have the interior angles on the same side of the transversal supplementary.
• Use common sense. While a diagram should never be used as proof of the dimensions of a figure, the parallelogram figure will show you that these two angles cannot be equal to one another. One angle is obtuse and the other angle is acute. |
|
| 6. |
|
Given: rhombus ABCD with diagonals drawn.
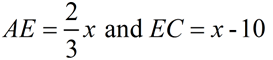
Find the value of x.
Solution:
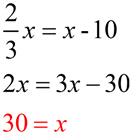 |
| |
Remember:
•
Don't let fractions throw you. Use your algebra skills! If you don't like working with the fraction, multiply each term of the equation by the denominator value to eliminate the fraction from the problem.
• While this problem gave you a rhombus, it was not expecting the use of a property specific to a rhombus. The needed property is that the diagonals bisect each other - a property held by both parallelograms and rhombuses. |
|
| 7. |
|
Given: trapezoid ABCD (not isosceles).
Which triangle is equal in area to ΔABD ?
Solution: The area of a Δ is ½bh. The area of ΔABD is ½(AD)(h). Since the perpendicular distance between parallel lines (the height) is constant (the same), the height measured from point B = height measured from point C. The area of ΔABD = the area of ΔACD (since both triangles have a base value of AD).
|
| |
Remember:
•
Use your powers of observation. Look carefully at the diagram. Think about what AREA entails (which is the use of the base and height of a triangle). Notice that several triangles can have base AD.
• Since you are given a trapezoid, parallel lines are most likely involved in the solution to this problem in some manner. Parallel lines are everywhere equidistant, making vertical height measurements within the trapezoid equal. |
|
| 8. |
|
Given: isosceles trapezoid BEAR as marked.
Find AQ.
Solution: Figure EAQC is a rectangle with CQ = 15. BR - CQ = 12, to be shared equally for BC and RQ, since ΔARQ 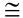 ΔEBC by HL. The missing side of ΔARQ has a length of 8 by Pythagorean Theorem. AQ = 8. ΔEBC by HL. The missing side of ΔARQ has a length of 8 by Pythagorean Theorem. AQ = 8.
|
| |
Remember:
•
It is often helpful to "decompose" a figure (break it into other shapes that can be more easily manipulated). In this problem, the trapezoid is divided into two right triangles and a rectangle.
• Don't forget your friend the Pythagorean Theorem. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|