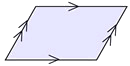
|
|
A parallelogram is a quadrilateral with both pairs of opposite sides parallel. |
 |
|
By using the definition, all of the parallelogram properties, when stated as theorems, can be "proven" true.
Remember, a definition is considered to be a true fact.
The parallelogram "property theorems" will be stated in "if ...then" form. Both the theorem and its converse (where you swap the "if" and "then" expressions) will be examined.
Click  in the charts below to see each proof.
The * indicates Theorems specifically stated in NY NGMS standards.
This does not imply these are the only theorems that should be studied, but they have been emphasized as important.
|
Use the following, when GIVEN a parallelogram: |
|
DEFINITION: A parallelogram is a quadrilateral with both pairs of opposite sides parallel. |
|
THEOREM: If a quadrilateral is a parallelogram, it has 2 sets of opposite sides congruent. |
 * |
|
|
|
THEOREM: If a quadrilateral is a parallelogram, it has 2 sets of opposite angles congruent. |
* |
|
|
THEOREM: If a quadrilateral is a parallelogram, it has consecutive angles which are supplementary. |
|
|
|
|
THEOREM: If a quadrilateral is a parallelogram, it has diagonals which bisect each other. |
* |
|
|
THEOREM: If a quadrilateral is a parallelogram, it has diagonals which form 2 congruent triangles. |
* |
|
|
Use the following, to PROVE a parallelogram: |
|
DEFINITION: A parallelogram is a quadrilateral with both pairs of opposite sides parallel. |
|
THEOREM: If a quadrilateral has 2 sets of opposite sides congruent, then it is a parallelogram. |
* |
|
|
|
THEOREM: If a quadrilateral has 2 sets of opposite angles congruent, then it is a parallelogram. |
* |
|
 |
THEOREM: If a quadrilateral has consecutive angles which are supplementary, then it is a parallelogram. |
|
|
|
|
THEOREM: If a quadrilateral has diagonals which bisect each other, then it is a parallelogram. |
* |
|
|
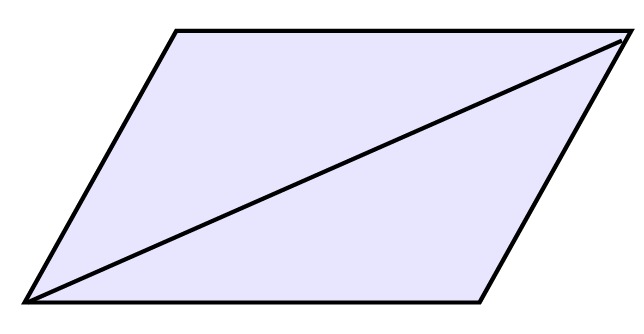
THEOREM: If a quadrilateral has diagonals which form 2 congruent triangles, then it is a parallelogram. |
* |
|
 |
 There is one additional theorem that combines two properties of the parallelogram.
This is a valuable theorem as it can make proving a parallelogram faster and easier.
|
|
THEOREM: If a quadrilateral has one set of opposite sides which are both congruent and parallel, then it is a parallelogram. |
|
This theorem can save time and energy when working a proof! |
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
