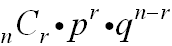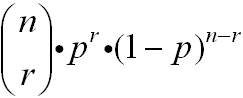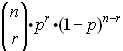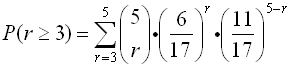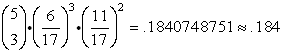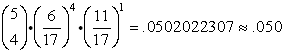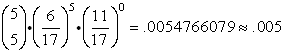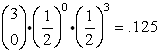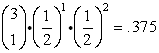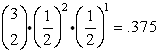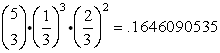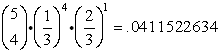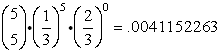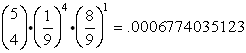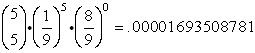|
When computing "at least" and "at most" probabilities, it is necessary to consider,
in addition to the given probability,
• all probabilities larger than the given probability ("at least")
• all probabilities smaller than the given probability ("at most") |
The probability of an event, p,
occurring exactly r times: |
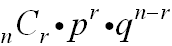
n = number of trials
r = number of specific events you wish to obtain
p = probability that the event will occur
q = probability that the event will not occur
(q = 1 - p, the complement of the event) |
|
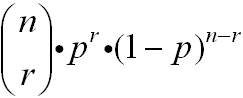 Alternative formula form Alternative formula form |
|

Illustration:
A bag contains 6 red Bingo chips, 4 blue Bingo chips, and 7 white Bingo chips. What is the probability of drawing a red Bingo chip at least 3 out of 5 times? Round answer to the nearest hundredth.
To solve this problem, we need to find the probabilities that r could be 3 or 4 or 5,
to satisfy the condition "at least".
It will be necessary to compute 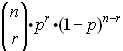
for r = 3, r = 4 and r = 5 (which means do the formula three times)
and add these three probabilities for the final answer.
Written in summation notation, we need to compute:
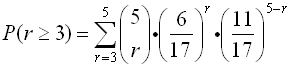
| For r = 3: |
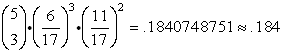 |
| For r = 4: |
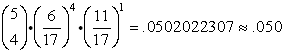 |
| For r = 5: |
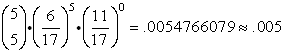 |
| Sum: |
0.184 + 0.050 + 0.005 = 0.239
rounded to the nearest hundredth = 0.24 ANS |
Note: it may be helpful to remember in this problem that
"at most 2 successes" is the compliment of "at least 3 successes".
In the following examples, answers will be rounded to the nearest hundredth.


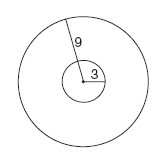
 As shown in the accompanying diagram, a circular target with a radius of 9 inches has a bull's-eye that has a radius of 3 inches. If five arrows randomly hit the target, what is the probability that at least four hit the bull's-eye? Express answer to the nearest thousandth. As shown in the accompanying diagram, a circular target with a radius of 9 inches has a bull's-eye that has a radius of 3 inches. If five arrows randomly hit the target, what is the probability that at least four hit the bull's-eye? Express answer to the nearest thousandth. |
|
Solution:
"At least" 4 hits implies 4 or 5 hits. The area of the bull's-eye is 9π and the area of the entire target is 81π. The probability of hitting the desired bull's-eye is 1/9.
| For r = 4: |
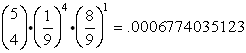 |
| For r = 5: |
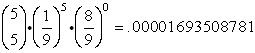 |
| Sum: |
rounded to the nearest thousandth = 0.001 ANS |
|

|
For working
with
Bernoulli Trials
on your
calculator,
click here. |
|
|
|
For working
with
At Most
At Least
on your
calculator,
click here. |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|