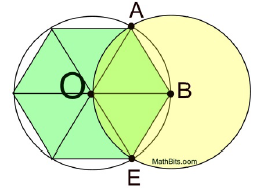
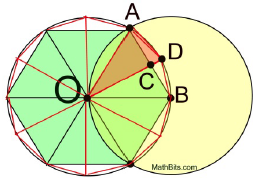
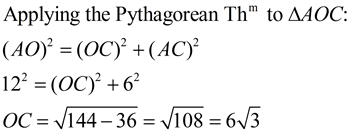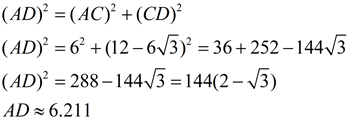For ease of computation, let's say that the length of the radius, AO, in this diagram equals 12 units. We know that AB = OA (radius), so AC, which is half of AB, equals 6.
The length AD (the side of the dodecagon) can be determined by Pythagorean Thm in ΔACD.
 |
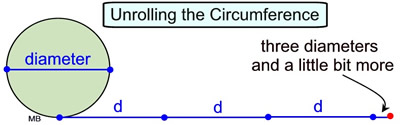
The perimeter of dodecagon = 12•(6.211) = 74.532. The circumference of circle O must be greater than 74.532, or greater than 6.211r. This shows π must be a little greater than 3.105.
We are getting closer to the actual value of π ! |
If we continue to increase the number of sides of the inscribed polygon, we will get closer to the actual circumference of the circle, and our solution for π will get closer to the actual value of 3.14159...

Like circumference, the area of a circle also deals with pi (π).
A = π • r2
Derivation of the Area Formula:
You have seen the derivation of this formula in past years. Here is a refresher:
We start knowing that the circumference of a circle is C = 2π • r, and that the area of a rectangle is A = bh.
A circle is divided into congruent sectors (pie slices). The sectors are pulled out of the circle and are arranged as shown in the middle diagram. The length across the top (over the curved arcs) is half of the circumference. When placed in these positions, the sectors form a parallelogram. The larger the number of sectors that are cut, the less curvy the arcs will appear and the more the shape will resemble a parallelogram. As seen in the last diagram, the parallelogram ca be changed into a rectangle by slicing half of the last sector and placing it to the far left.
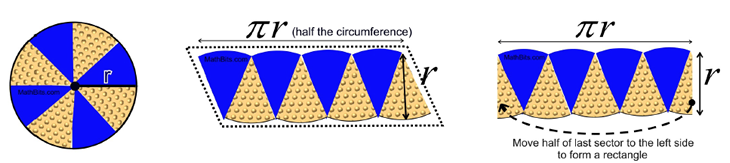
The area of the rectangle is A = bh.
Thus, the area of the sectors that make up the rectangle is πr • r = π • r2.