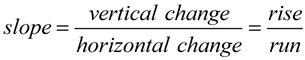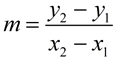The slope of a line, m, is a rate of change which is constant in linear equations.
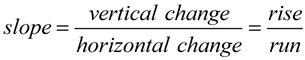
or expressed as = 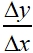
described as
"delta y over delta x"
"delta", Δ, is a Greek letter meaning "change in".
When a line passes through the points
(x1, y1) and (x2, y2), the slope, m, is expressed:
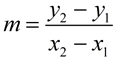
Slopes may be positive, negative, zero, or undefined(does not exist).
 |
Lines that have positive slope, rise from the lower left to the upper right on the axes. They go "up hill". |
 |
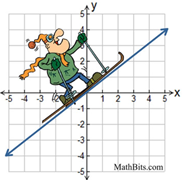
Lines that have negative slope, decline from the upper left to the lower right on the axes. They go "down hill". |
 |
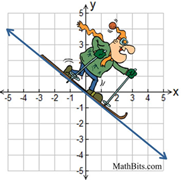
Lines that are horizontal have a slope of zero.
(There is no "rise" which creates a zero numerator.)
|
 |
Lines that are vertical have no slope (undefined slope).
(There is no "run" which creates a zero denominator.) |
|
Depending upon the given information, equations of lines can take on several forms:
• Slope Intercept Form:
y = mx + b
Use this form when you know, or can find, the slope, m, and the y-intercept, b.
• Point Slope Form:
y - y1 = m(x - x1)
Use this form when you know, or can find, a point on the line (x1, y1), and the slope, m.

• Standard Form:
Ax + By = C
The A and B values in this form cannot be zero. Use when asked to state the answer in Standard Form.
May also be Ax + By - C = 0.
• Horizontal Line Form (left/right):
y = 7 (or any Real number)
• Lines that are horizontal have a slope of zero.
• They are parallel to the x-axis.
• They have "run", but no "rise". The rise/run formula for slope always yields zero since rise = 0.
• Every point on this line has a y-value of 7.
• When writing the equation, we have
y = mx + b
y = 0x + 7
y = 7.
• Note: The equation of the x-axis is y = 0.
• Vertical Line Form (up/down):
x = -5 (or any Real number)
• Lines that are vertical have no slope (it does not exist, undefined).
• They are parallel to the y-axis.
•
They have "rise", but no "run". The rise/run formula for slope always has a zero denominator and is undefined.
•
Every point on this line has an x-value of -5.
•
Note: The equation of the y-axis is x = 0.
|