|
Directions: Read carefully and choose the best answer.
1. |
Write the equation of a circle whose center is at (3,-2) and has a radius of 11. |
|
|
|
2. |
Given the equation of a circle,
(x - 5)2 + (y + 3)2 = 196,
state the coordinates of the center and the radius. |
|
|
Choose:
|
|
3. |
State the coordinates of the center and the radius of a circle whose equation is
x2 + y2 + 2x - 4y - 11 = 0 . |
|
|
|
4. |
Graph the circle: x2 + 10x + y2 - 6y = - 30.
| |
|
5. |
Write the equation of a circle whose center is (-4,8) and passes through the point (-2,-1). |
|
|
|
|
Write the general equation of a circle that is tangent to the x-axis, with a center located at (4,-6).
| 
| |
7. |
Show that the point 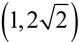 lies on a circle whose center is the origin and contains the point (0,3). lies on a circle whose center is the origin and contains the point (0,3).
|
|
|
8. |
The equation x2 + y2 - 12x - 8y + 27 = 0 is equivalent to: |
|
|
|
9. |
A regular hexagon ABCDEF with a side length of 4 units is centered at G(5,3). State the general equation of the circle circumscribing the hexagon. |
|
|
|
10. |
Which of the equation choices could represent the circle shown on the graph?
(Check all that apply, and hit SUBMIT!) |
| |
|
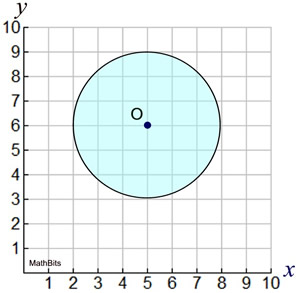 (Assume a radius of integer length.)
(Assume a radius of integer length.) |
11. |
The equation x2 + y2 - 6x + 4y = d
describes a circle.
a) Determine the y-coordinate of the center of the circle.
b) The radius of the circle is 6 units. What is the value of "d" in the given equation.
|
|
|
|
12. |
Given circle: x2 - 9x + y2 = 4.75
In center-radius form, this equation will be written as:
|
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|