|
Directions: Prepare a coordinate geometry proof for each problem. Some problems specify a method, while others leave the choice of method up to you. While more than one method of proof, or presentation, is possible, only one possible answer will be shown for each question.
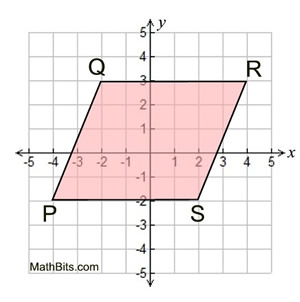
1. |
Given: quadrilateral PQRS with
P(-4,-2), Q(-2,3), R(4,3) and
S(2,-2).
Prove: PQRS is a parallelogram using slopes.
|
|
|
2. |
Given: ΔDOG with D(-2,5), O(-4,1) and G(-10,4)
Show: ΔDOG is a right triangle
|
 |
|
3. |
Given: quadrilateral FRED with
F(0,3), R(4,5), E(5,3) and D(1,1)
Prove: FRED is a rectangle
|
 |
|
4. |
Given: quadrilateral ABCD with
A(5,1), B(0,3), C(-2,5) and D(3,3)
Show: ABCD is a parallelogram
using midpoints.
|
 |
|
5. |
Given: quadrilateral CDEF with
C(-2,3), D(-5,-4), E(2,-1) and
F(5,6)
Prove: CDEF is a rhombus but not a square
|
 |
|
6. |
Given: ΔFUN with F(4,-1), U(5,6) and N(1,3)
Show: ΔFUN is an isosceles right triangle
|
 |
|
7. |
Given: quadrilateral TRAP with
T(-5,7), R(-3,-4), A(9,5) and P(-1,10)
Show: TRAP is an isosceles trapezoid
|
 |
|
8. |
Given: quadrilateral ARMY with
A(p,q), R(0,0), M(r,0) and Y(p+r,q)
Prove ARMY is a parallelogram.
|
 |
|
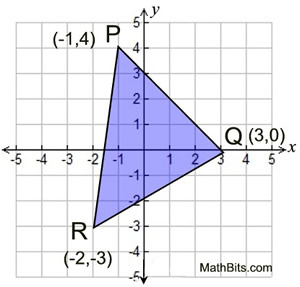
9. |
Given: ΔPQR with P(-1,4), Q(3,0),
and R(-2,-3)
Prove ΔPQR is NOT a right triangle.
|
 |
|
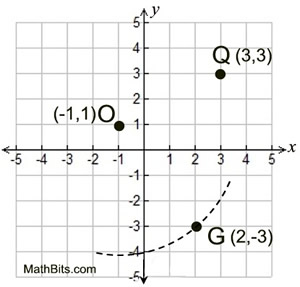
10. |
Given: Circle O with center at
(-1,1) and point G(2,-3) lies on the circle.
Create a proof to show whether point Q(3,3) lies on the circle, or not.
|
 |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|