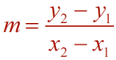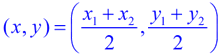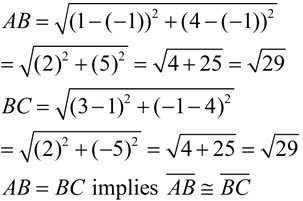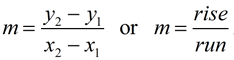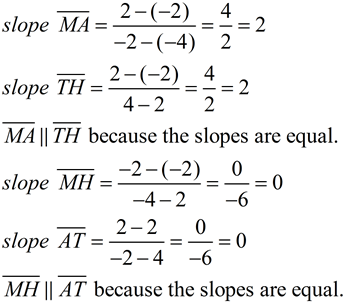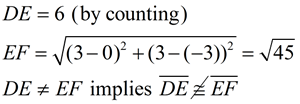|
Seventeenth century French mathematician Rene Descartes applied algebra principles to geometric situations. This blending of algebra and geometry is referred to as analytic geometry. Since this process often involves placing geometric figures in a coordinate plane, it is commonly known as coordinate geometry.
Coordinate geometry proofs employ the use of formulas such as the Slope Formula, the Midpoint Formula and the Distance Formula, as well as postulates, theorems and definitions.
Slope Formula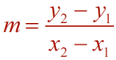 |
Midpoint Formula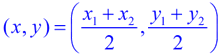 |
Distance Formula
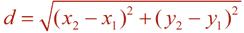 |
When developing a coordinate geometry proof: |
1. Plot the points, draw the figure and label.
2. State the formulas you will be using.
3. Show ALL work.
4. Have a concluding sentence stating what you have proven and why it is true. Usually a theorem or a definition is needed here.
|
 |
Remember that problems asking you to "PROVE" or "SHOW" are asking for a proof and your response should be well detailed. |
|
|
If a problem asks you to "PROVE" or "SHOW" some statement, it means that the statement is CORRECT as stated. If your work does not agree with the statement, you have made a mistake somewhere in your work. Check your work again. |
|

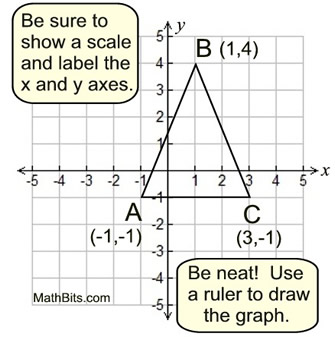
Given: ΔABC with A(-1,-1), B(1,4) and C(3,-1)
Show:
ΔABC is isosceles
|
Always read the question carefully for hints. The word isosceles, by definition, implies 2 congruent sides in ΔABC. Congruent means "of equal length", so the Distance Formula is needed. |
|
Always draw a neat, labeled graph for the problem. Show a scale and label the x and y axes. Use a ruler to draw straight lines or segments. A folded piece of paper will work as a ruler for drawing. |
|
State the formula you will be using. |
|
Show ALL work!! Since isosceles triangles have two congruent sides, we can stop when we find the two sides. Always look at the figure and take your best guess as to which two sides may be congruent.
Remember that this triangle IS isosceles! |
The triangle is isosceles because
it has two congruent sides. |
Conclude with a statement justifying why you know the triangle is isosceles. Think of using a theorem or a definition for this statement. |

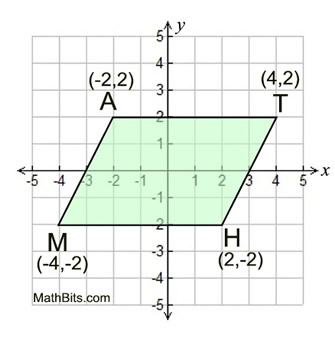
Given: quadrilateral MATH; M(-4,-2), A(-2,2),
T(4,2) and H(2,-2)
Prove: MATH is a parallelogram
|
This question is looking for a parallelogram. There are several different ways to prove a quadrilateral is a parallelogram. Since no specific method is requested, use any method of choice. We will be showing 2 sets of parallel sides, using slope. |
|
A neat, labeled drawing is prepared. |
|
State the formula you will be using. |
|
Show ALL work!! Remember that "2 sets" of parallel sides actually means 4 sides.
The slopes of the horizontal sides could simply be stated as being equal to zero, since all horizontal segments have a slope of zero (no rise).
Remember that this figure IS a parallelogram.
|
Since the slopes are equal, we know that the sides are parallel. MATH is a parallelogram because it is a quadrilateral with two sets of parallel sides. |
Be sure to make the connection between equal slopes and parallel segments. Then conclude with the theorem (or definition) regarding the opposite sides being parallel. |

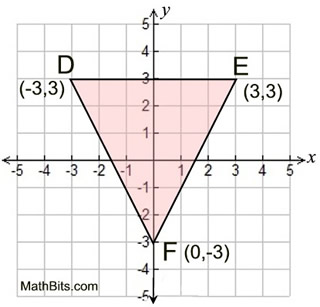
Given: Δ DEF with D(-3,3), E(3,3), F(0,-3)
Show: Δ DEF is NOT an equilateral triangle
|
This question is asking you to prove that the triangle is NOT equilateral. You need to find something about the triangle that contradicts the concept of "equilateral". Look for a side that is not equal in length to the other sides. |
|
A neat, labeled drawing is prepared. |
|
State the formula you will be using. |
|
Show ALL work!! Remember that "you are looking for a contradiction".
As soon as you find a contradiction, you will be finished.
|
An equilateral triangle has three congruent sides. Since two sides of this triangle are not congruent, this is NOT an equilateral triangle. |
Be sure to clearly state what you found that contradicts the concept of "equilateral", and what the concept of "equilateral" actually means. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|