Square MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

Use only your compass and straight edge when drawing a construction. No free-hand drawing!

We will be doing TWO constructions of a square. The first will be to construct a square given the length of one side, and the other will be to construct a square inscribed in a circle.

Given: the length of one side of the square Construct: a square

STEPS:
1. Using your straightedge, draw a reference line, if one is not provided.
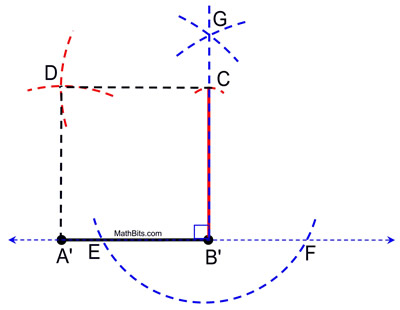
2. Copy the side of the square onto the reference line, starting at a point labeled A'.
3. Construct a perpendicular at point B' to the line through .
4. Place your compass point at B', and copy the side of the square onto the perpendicular . Label the end of the segment copy as point C.
5. With your compass still set at a span representing AB, place the compass point at C and swing an arc to the left.
6. Holding this same span, place the compass point at A' and swing an arc intersecting with the previous arc. Label the point of intersection as D.
7. Connect points A' to D, D to C, and C to B' to form a square.

Proof of Construction: As a result of the construction of the perpendicular at B', m∠A'B'C = 90º, since perpendicular lines meet to form right angles, and a right angle contains 90º. By copying the segment length of the side of the square, , we have A'B' = B'C = CD = DA'. A figure having four congruent sides and an interior angle which is a right angle, is a square.

STEPS:
1. Using your compass, draw a circle and label the center O.
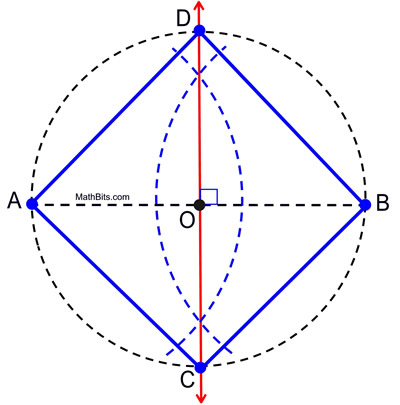
2. Using your straightedge, draw a diameter of the circle, labeling the endpoints A and B.
3. Construct the perpendicular bisector of the diameter, .
4. Label the points where the bisector intersects the circle as C and D.
5. Connect points A to B to C to D to form the square.

Proof of Construction: is a diameter of the circle since it passes through the center of the circle. From the construction of the perpendicular bisector of , we know that O is the center of (and the center of the circle), making also a diameter of the circle. In addition, . Since both and are diameters, we have radii AO = BO = CO = DO showing that and bisect each other. Since the diagonals bisect each other, ABCD is a parallelogram. And since diameters of a circle are congruent, we also know that the diagonals of ABCD are congruent and perpendicular, making ABCD a square.