Intuitively, the word "circumscribed", in geometry, refers to drawing a shape around
the outside of another shape so the interior shape "fits snugly" inside of the outside shape.
circumscribe is like circumference See the discussion on "circumcenters" at Circumcenter - Concurrent Bisectors.
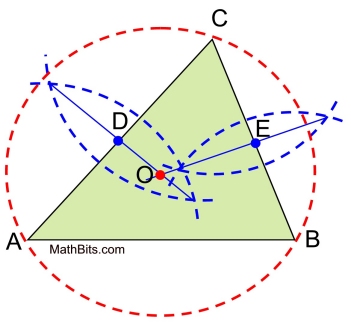
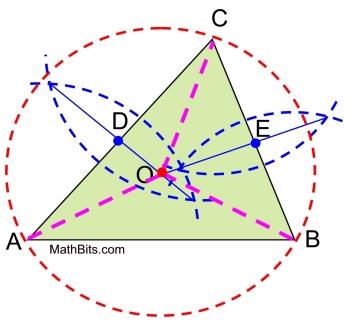
This construction will focus on the perpendicular bisectors of the sides of the triangle. Remember the theorem: "Any point on a perpendicular bisector of a segment is equidistant from the ends of the segment." Where the perpendicular bisectors intersect (say point O), will be used to establish that OA = OB = OC as the radii of a circle around the outside of the triangle.
Steps:
1. Construct the perpendicular bisectors of at least two sides of the triangle. 2. Place a dot point where the two perpendicular bisectors intersect. This will be the center of your circumscribed circle, O. 3. Place the compass point on the point of intersection (dot) and measure from the center to one of the vertices of the triangle, to determine the radius of the circumscribed circle. 4. Draw the circumscribed circle.
• Why is it sufficient to only construct the perpendicular bisectors of TWO sides of the triangle, instead of all three sides? Only two perpendicular bisectors will be needed, since when OA = OC and OB = OC, the substitution (or transitive) property gives us that OA = OB, and we have all three radii equal in length, OA = OB = OC. It is not necessary to have the third perpendicular bisector, since we already know mathematically that OA = OB. Yes, you can construct the third perpendicular bisector, if you wish, to verify the location of point O.
Proof of Construction: Draw radii from O to C, from O to A and from O to B. Since point O lies on the perpendicular bisector of
Topical Outline | Geometry Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|