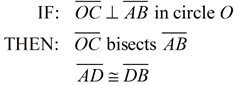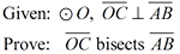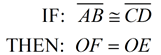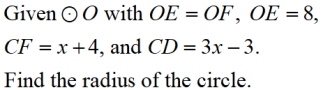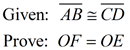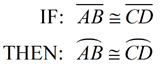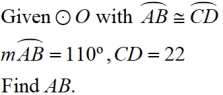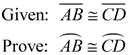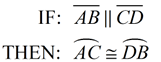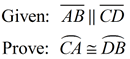|
This lesson deals with theorems associated with the positions and locations of chords in circles.
These theorems will be valuable when working with applications of circles,
and when proving other relationships related to circles.

|
A chord is a segment that joins two points of a circle. |
|
|
A diameter is a chord that contains the center of the circle. |
|
|
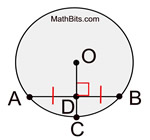
In a circle, a radius perpendicular to a chord bisects the chord. |
Converse: |
In a circle, a radius that bisects a chord is perpendicular to the chord. |
Also stated: |
In a circle, the perpendicular bisector of a chord passes through the center of the circle |
Extended form: |
In a circle, a diameter perpendicular to a chord bisects the chord and its arc. |
| |
|
|
|
Example:

|
Solution:
• As a radius, OC = 10.
OC = OD + DC
If DC = 4, the OD = 6.
• ΔADO is a right triangle with leg = 6 and hypotenuse = 10. By Pythagorean Theorem, the other leg, AD = 8.
• Since the radius is perpendicular to the chord, it bisects the chord. Thus AB = 16. |
|
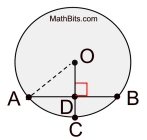
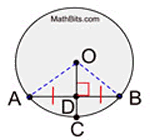
PROOF:
|
Proof:

|
|
Proof of the converse is left as an exercise.

|
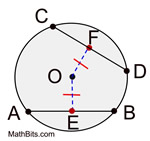
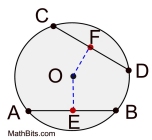
In a circle, or congruent circles, congruent chords are equidistant from the center. |
Converse: |
In a circle, or congruent circles, chords equidistant from the center are congruent. |
| |
|
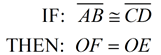
NOTE: The term "equidistant", in this theorem, refers to the perpendicular distance from the center of the circle to the chord.
|
|
Example:
|
Solution:
• Since OF = OE, the chords are congruent.
Remember that these distances mark segments that are perpendicular to their respective chords, (and bisect the chords from the previous theorem).
CF = CD
2(x + 4) = 3x - 3
2x + 8 = 3x - 3
11 = x
CF = x + 4 = 15
• ΔOFC is a right triangle with leg = 15 and a leg of 8. By Pythagorean Theorem, the hypotenuse, OC (radius) = 17. |
|
PROOF:
|
Proof:

|
|
Proof of the converse is left as an exercise.

|
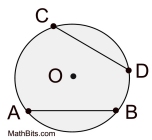
In a circle, or congruent circles, congruent chords have congruent arcs. |
Converse: |
In a circle, or congruent circles, congruent arcs have congruent chords. |
| |
|
|
|
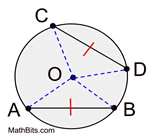
Example:
|
Solution:
• Since the arcs are congruent, the chords that intercept these arcs are also congruent. Thus, we know that AB = CD.
CD = 22
AB = 22. |
|
PROOF:
|
Proof:
|
|
Proof of the converse is left as an exercise.

|
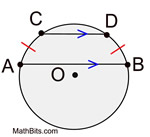
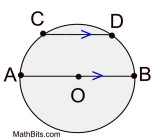
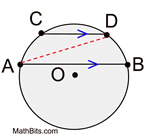
In a circle, parallel chords intercept congruent arcs |
| |
|
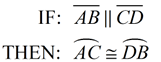 |
|
Example:
|
Solution:
• Since the chords are parallel, the intercepted arcs are congruent.
• The arc from A through C and D to B is a semicircle = 180º.
58 + 58 + x = 180
x = 64º
• The measure of the arc from C to D is 64º |
|
PROOF:
|
Proof:
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|