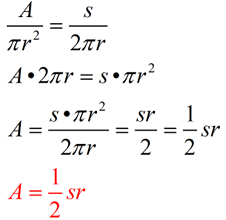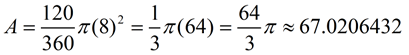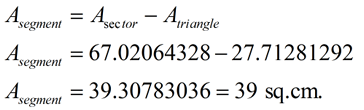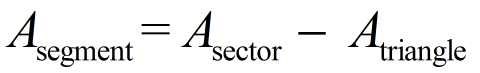|
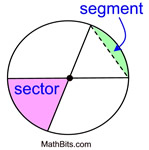
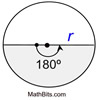
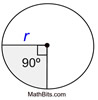
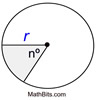
Sector of a circle: A sector of a circle is the portion of a circle enclosed by two radii and an arc. It resembles a "pizza" slice.
|
|
When finding the area of a sector, you are actually finding a fractional part of the area of the entire circle. The fraction is determined by the ratio of the central angle of the sector to the "entire central angle" of 360 degrees. [frational part = 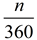 ; where n = central angle]
; where n = central angle]
It is also possible to find the area of a sector by expressing the fraction as the
ratio of the arc length (s) to the entire circumference. 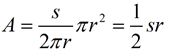

1. Find the area of a sector with a central angle of 40º and a radius of 12 cm. Express answer to the nearest tenth.
Solution:
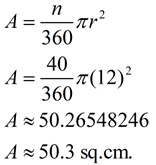 |
2. Find the area of a sector with an arc length of 30 cm and a radius of 10 cm.
Solution:
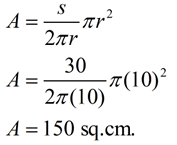
|

We have seen that the area of a sector is a fractional part of the area of the entire circle. The area of a sector can be expressed using its central angle or its arc length.
The following proportions are true regarding the sector:
 |
 |
We are going to derive the formula for the area of a sector using the sector's arc length.
Using the first and last ratios in the proportion shown above, the following is true.
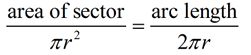
If A = area of the sector, and s = arc length, then 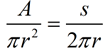 .
.
Solving the proportion for A gives:
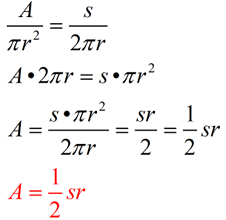

|
Segment of a Circle: The segment of a circle is the region bounded by a chord and the arc subtended by the chord. |
|
While a sector looks like a "pie" slice, a segment looks like the "pie" slice with the triangular portion cut off (it's somewhat like the "crust section of the pizza slice"). The segment is the small partially curved figure left when the triangular portion of the sector is removed.
|
 |
|
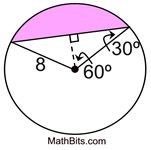
Find the area of a segment of a circle with a central angle of 120 degrees and a radius of 8 cm. Express answer to the nearest integer.
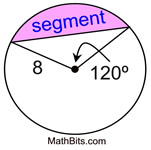
|
Solution:
Start by finding the area of the sector.
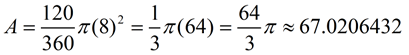
Now, find the area of the triangle. Dropping the altitude from the center forms a 30-60-90 degree triangle. Using the 30-60-90 rules (or trigonometry), find the altitude, which is 4, and the other leg, which is 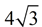 or 6.92820323. or 6.92820323.
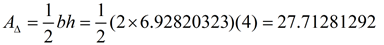
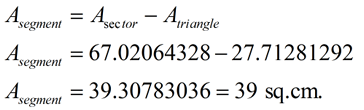
|
|
|
|



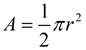
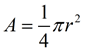
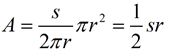
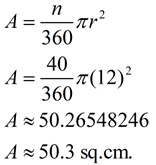
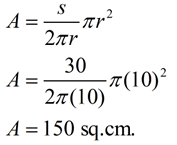


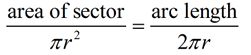
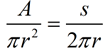 .
.