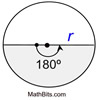
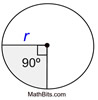
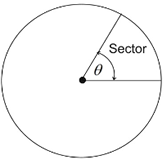
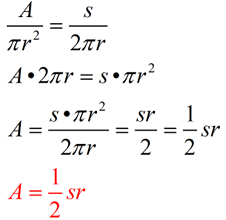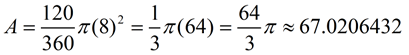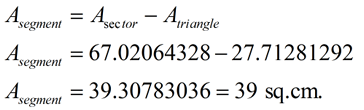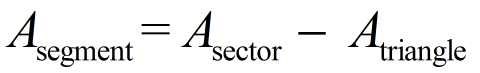Common sectors in circles: ("A" represents AREA of sector):
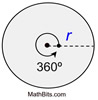
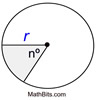
The area of a sector is found using proportionality (establishing a "fractional part"). Method 1: Calculating the Area of a Sector when the Central Angle is known: When finding the area of a sector (using the central angle and radius), you are actually finding The "fractional part" is the ratio of the central angle of the sector [fractional part =
Method 2: Calculating the Area of a Sector when the Arc Length and Radius are known: When finding the area of a sector (using the arc length and radius),
We are going to derive the formula for the area of a sector using the sector's arc length. If A = area of the sector, and s = arc length, then Solving the proportion for A gives:
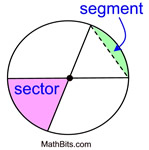
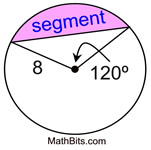
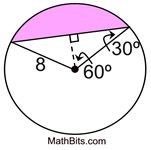
 You can probably "guess" what the formula for finding the area of a segment involves. A segment is a sector with the triangular portion removed. Formula: Area of Segment = Area of Sector - Area of Triangle
Topical Outline | Geometry Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|
||||||||||||||||||||||||||||

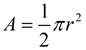
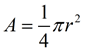
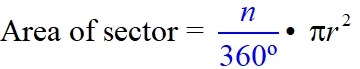
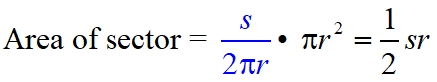
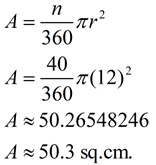
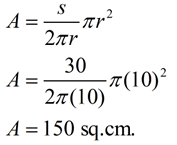

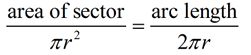
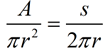 .
.