|
An arc of a circle is a "portion" of the circumference of the circle.
The length of an arc is simply the length of its "portion" of the circumference. The circumference itself can be considered a full circle arc length. |
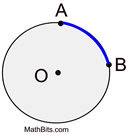 |

As you progress in your study of mathematics and angles, you will see more references made to the term "radians" instead of "degrees". So, what is a "radian" ?
|
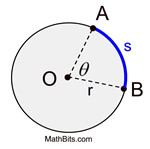
The radian measure, θ, of a central angle is defined as the ratio of the length of the arc |
the angle subtends, s, divided by the radius of the circle, r. |
|
which gives arc length, s: s = θr
|
 subtend = "to be opposite to"
subtend = "to be opposite to"
|
One radian is the central angle that subtends an
arc length of one radius (s = r).
Since all circles are similar, one radian is the same value for all circles. |

| Relationship between Degrees and Radians: |
In a circle, the arc measure of the entire circle is 360º and the arc length of the entire circle is represented by the formula for circumference of the circle:  . .
Substituting C into the formula s = θr shows:
C = θr 2πr = θr 2π = θ
The arc measure of the central angle of an entire circle is 360º and the radian measure of the central angle of an entire circle = 2π.
360º (degrees) = 2π (radians)
|
|
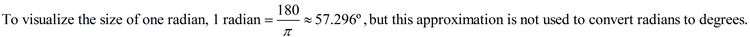
To change
from degrees to radians,
multiply degrees by  |
|
To change
from radians to degrees,
multiply radians by 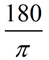 |
|

Arc Length and Radian Measure |
While we are familiar with using degrees to represent angles,
using radians may simplify formulas such as the formula for finding arc length.
In radians,
arc length, s: s = θr
θ = angle in radians, r = radius of circle.
|

1. Find the length of an arc subtended by an angle of 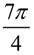 radians in a circle of radius 20 centimeters. radians in a circle of radius 20 centimeters.
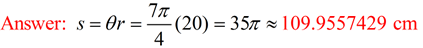 |
So, what would this problem look like if we used degrees?
First, change the angle 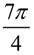 radians into degrees. radians into degrees. 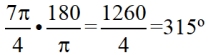
Arc length formula with degrees: 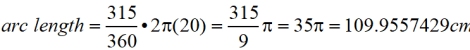 Using the radian formula was faster, since the angle was in radians.
Using the radian formula was faster, since the angle was in radians. |
2. Find the arc length in a circle of radius 12 cm with a central angle of 1.2 radians.
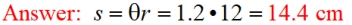 |
3. Find the length of the minor arc from point A to point B, when the radius of the circle is 8 feet and the central angle is expressed in radians.
Give the exact answer (do not round).
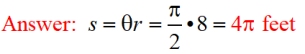 |
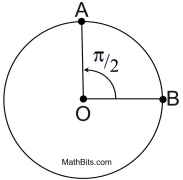 |

Justify why (in relation to radians): The length of the arc intercepted by a central angle is proportional to the radius. |
The diagram at the right shows two circles with the same center (concentric circles). It has already been shown that concentric circles are similar under a dilation transformation.
The ratio of similitude of the smaller circle to the larger circle is:
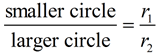 |
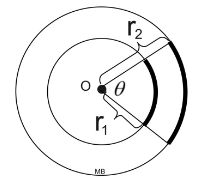 |
| The same dilation that mapped the smaller circle onto the larger circle will also map the slice (sector) of the smaller circle with an arc length of s1 onto the slice (sector) of the larger circle with an arc length of s2. When the radius gets dilated by a scale factor, the arc length is also dilated by that same scale factor. |
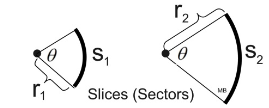 As long as the central angles are the same, the slices (sectors) will be similar. |
Since corresponding parts of similar figures are in proportion, 
An equivalent proportion can be written as 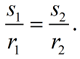 This proportion shows that the ratio of the arc length intercepted by a central angle to the radius of the circle will always yield the same (constant) ratio. This proportion shows that the ratio of the arc length intercepted by a central angle to the radius of the circle will always yield the same (constant) ratio.
In relation to the two arc length formulas seen on this page, both show that arc length, s, is expressed as "some value" times the radius, r. The arc length is proportional to the radius.
When the angle θ is in radians:
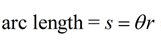
|
Setting r = 1 shows the constant of proportionality.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|


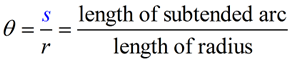

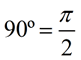
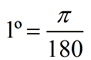
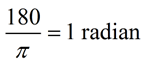

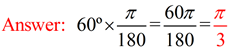
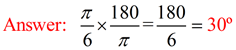

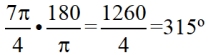
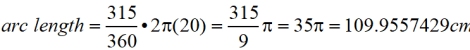
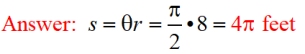

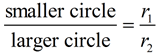

 As long as the central angles are the same, the slices (sectors) will be similar.
As long as the central angles are the same, the slices (sectors) will be similar. 
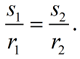 This proportion shows that the ratio of the arc length intercepted by a central angle to the radius of the circle will always yield the same (constant) ratio.
This proportion shows that the ratio of the arc length intercepted by a central angle to the radius of the circle will always yield the same (constant) ratio.