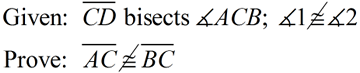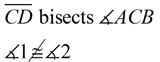|
When trying to prove a statement or theorem to be true, it may be beneficial to ask "What if this statement or theorem was not true?" and examine what happens. This concept is the premise of the Indirect Proof, or Proof by Contradiction.
Indirect Proof:
Assume what you need to prove is false, and then show that something contradictory (absurd) happens. |
Proof by Contradiction is also known as reductio ad absurdum
(which from Latin means reduced to an absurdity). |
Assumption Made by an Indirect Proof: If all possible conclusions to a proposition are listed, one of them must be true, and if all but one are proved false, then the remaining conclusion is true.
Steps in an Indirect Proof:
• |
Assume that the opposite of what you are trying to prove is true. |
• |
From this assumption, draw conclusions about the problem. Be sure that your conclusions are based on the assumption and the use of valid statements. |
• |
Look for a conclusion that you know will be false because it contradicts the Given, or known, information. Usually you will be contradicting "Given" information. |
• |
When the assumption leads to a false conclusion, the assumption must be false. |
• |
If the assumption (which is the opposite of what you are trying to prove) is false, then you will know that what you are trying to prove must be true. |
How to Recognize When an Indirect Proof is Needed:
Look for the word "not" or a "not symbol" in the problem. The presence of "not" or a "not symbol", such as the not equal 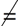 , or not congruent , or not congruent 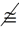 symbols, in a problem indicates a need for an Indirect Proof. symbols, in a problem indicates a need for an Indirect Proof.
Example:
Indirect Proof in Two - Column Format
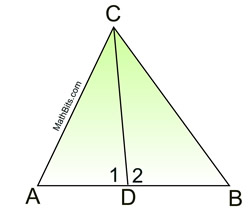
|
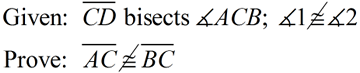
Notice how this problem is dealing with "NOT".
|
Statements |
Reasons |
|
1. |
|
|
1. |
Given |
2. |
|
2. |
Assumption leading to a contradiction. |
3. |
|
3. |
An angle bisector is a ray in the interior of the angle forming 2 congruent angles. |
4. |
|
4. |
Reflexive (Identity) - A quantity is congruent to itself. |
5. |
|
5. |
SAS - If 2 sides and the included ∠ of one Δ are congruent to the corresponding parts of another Δ, the Δ s are congruent. |
6. |
|
6. |
CPCTC - Corresponding parts of congruent triangles are congruent. |
7. |
|
7. |
Contradiction steps 1 and 6
QED |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|