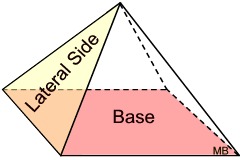
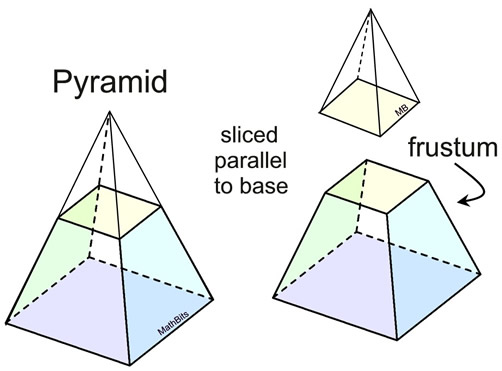
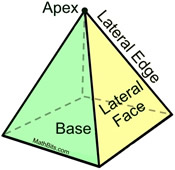
Pyramids are named for the shapes of their bases.
Volume of a Pyramid (for both right and oblique pyramids):
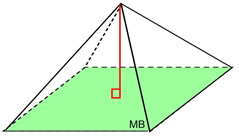
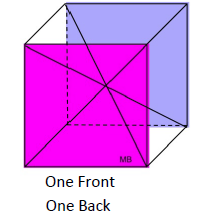
Justification of formula by "dissecting a cube":
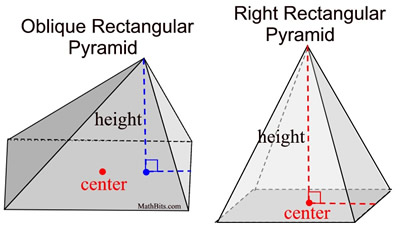
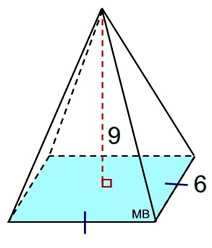
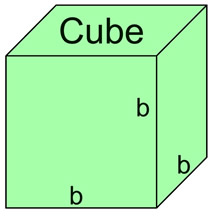
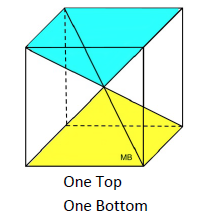
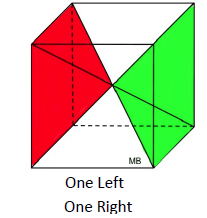
A total of 6 pyramids can fit inside this cube, as long as the pyramids' bases are the same as the base of the cube, and the heights of the pyramids are half the height of the cube (b). So the volume of one pyramid is one-sixth the volume of the cube. This dissecting a cube into 6 congruent pyramids only works because the height of the pyramid is half the height of the cube. What happens if the height is not half the height of the cube? We will need the formula to contain a variable to deal with the height of the pyramid. Since h = ½ b, we have 2h = b. Using substitution, we get: This new formula, This formula can be generalized to the statement: "the volume of a pyramid is equal to one-third the volume of a prism (V = Bh) with the same base and height as the pyramid." So, the volume of a pyramid formula generalizes to
 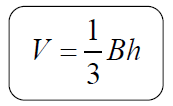
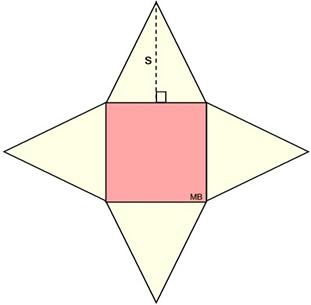
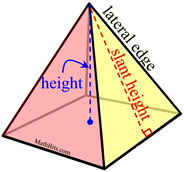
Surface Area of a Pyramid:
Topical Outline | Geometry Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|
||||||||||||||||||||||||||||||||||||||||||||||||||||

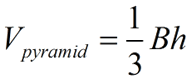
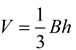 .
.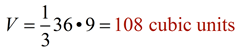
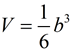
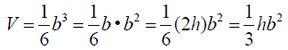 .
.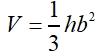 , says the
, says the