|
A Platonic solid is a regular convex polyhedron in which the faces are congruent regular polygons with the same number of faces meeting at each vertex. (The sum of the internal angles at each vertex is less than 360º.) |
|
There are FIVE (and only five) Platonic solids:
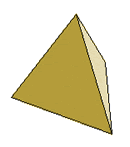
Tetrahedron |
Octahedron |
Icosahedron |
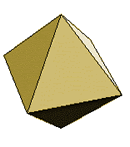
Cube |
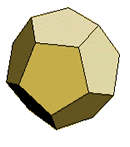
Dodecahedron |
|
 |
 |
 |
 |
The ancient Greek philosopher Plato c. 360 B.C. theorized that the classical elements of the world were made of these regular solids. The five Platonic Solids were thought to represent the five basic elements: earth, air, fire, water, and the universe.
• The cube is associated with the earth, and reconnecting energy to nature.
• The octahedron is associated with air, and cultivating acceptance and compassion.
• The tetrahedron is associated with fire, and perpetuates balance and stability.
• The icosahedron is associated with water, and enhances creative though and expression.
• The dodecahedron is associated with the universe, and represents mystery and meditation. Plato stated that the dodecahedron was "used for arranging the constellations on the whole heaven." The dodecahedron can be seen as representing the universe with the twelve zodiac signs corresponding to the twelve faces of the dodecahedron. |
These regular solids occur in areas such as chemistry, crystallography, mineralogy, oceanography, medical virology, cytology (the study of cells), geology, meteorology, astrology, electronics, and architecture, to name only a few. The Platonic solids can be described as forming the basis of all structure.
Platonic Solids:
(see the Platonic Solids nets)
Tetrahedron
|
A tetrahedron is formed by placing three equilateral triangles at a vertex (sum of angles at vertex is 180°).
It has 4 vertices, 6 edges, and 4 faces.
Each face is an equilateral triangle.
Of the Platonic solids, the tetrahedron has the smallest volume for its surface and is the only one that has fewer than five faces. It is one kind of a pyramid.
|
|
Octahedron |
An octahedron is formed by placing four equilateral triangles at each vertex (sum of angles at vertex is 240º).
It has 6 vertices, 12 edges, and 8 faces.
Each face is an equilateral triangle.
The octahedron rotates freely when held by its two opposite vertices.
|
|
Icosahedron |
An icosahedron is formed by placing five equilateral triangles at each vertex (sum of angles at vertex is 300°).
It has
12 vertices, 30 edges, and 20 faces.
Each face is an equilateral triangle.
Of the Platonic solids, it has the largest volume for its surface area.
|
|
Hexahedron
 |
A hexahedron, or cube, is formed by placing three squares at each corner (sum of angles at vertex is 270°).
It has 8 vertices, 12 edges, and 6 faces.
Each face is a square.
The cube has eleven possible nets. To color a cube so no two adjacent faces are the same color, require at least three colors.
|
|
Dodecahedron
|
A dodecahedron is formed by placing three regular pentagons at each vertex (sum of angles at vertex is 324°).
It has 20 vertices, 30 edges, and 12 faces.
Each face is a regular pentagon.
A dodecahedron has 160 possible diagonals.
|
|
Animated solids used with permission of creator Rüdiger Appel (all rights reserved).

<
Platonic Solids in Action:

This playground climbing device, comprised of five dodecahedrons,
can be found in a park on Lake Neatahwanta, in Fulton, New York.
There is a regular hexagon painted on each of the dodecahedron's regular pentagonal faces.

Due to the fact that each of their faces are the same, the Platonic solids make good dice.
Different types of games may use four-sided dice (tetrahedrons), six-sided dice (cubes), eight-sided dice (octahedrons), twelve-sided dice (dodecahedrons) and even twenty-sided dice (icosahedrons).














