|
The section Unit Circle showed the placement of degrees and radians in the coordinate plane. Angles in the unit circle start on the x-axis and are measured counterclockwise about the origin. While these unit circle concepts are still in play, we will now not be "drawing" the unit circle in each diagram. Our diagrams will now allow us to work with radii exceeding the unit one (as seen in the unit circle). |
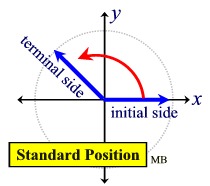
Standard Position: An angle is in standard position if its vertex is located at the origin and one ray is on the positive x-axis. The ray on the x-axis is called the initial side and the other ray is called the terminal side. If the terminal side of an angle lies "on" the axes (such as 0º, 90º, 180º, 270º, 360º ), it is called a quadrantal angle. The angle shown at the right is referred to as a Quadrant II angle since its terminal side lies in Quadrant II.
|
|
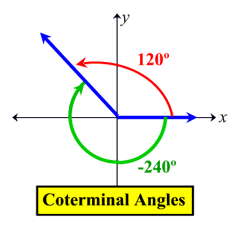 |
The angle is measured by the amount of rotation from the initial side to the terminal side. If measured in a counterclockwise direction the measurement is positive. If measured in a clockwise direction the measurement is negative. (A negative associated with an angle's measure refers to its "direction" of measurement, clockwise.)
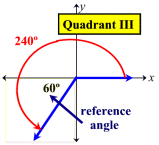
If two angles in standard position have the same terminal side, they are called coterminal angles. In the diagram at the left, +120º and -240º are coterminal angles. |
|

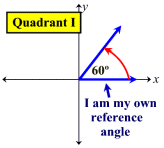
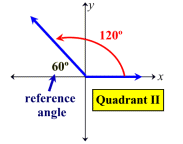
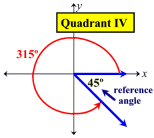
Reference Angles: Associated with every angle drawn in standard position (except quadrantal angles) there is another angle called the reference angle. The reference angle is the acute angle (the smallest angle) formed by the terminal side of the given angle and the x-axis. Reference angles may appear in all four quadrants. Angles in quadrant I are their own reference angles.
A reference angle is always positive and is always less than 90º.
Remember: The reference angle is measured from the terminal side of the original angle "to" the x-axis (not "to" the y-axis).

 If the starting angle is greater than 360º, start by subtracting 360º from the starting angle (as many times as needed) to arrive at a new "starting" angle that lies between 0º and 360º. If the starting angle is greater than 360º, start by subtracting 360º from the starting angle (as many times as needed) to arrive at a new "starting" angle that lies between 0º and 360º.
(If working in radians, subtract 2π until the starting angle is between 0 and 2π radians.)
Example: starting angle 460º becomes 460 - 360 = 100º starting angle.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|