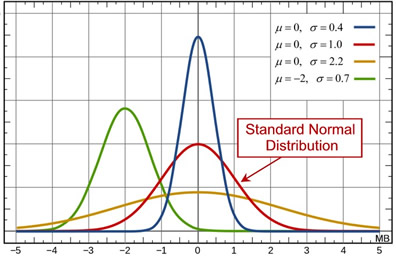
There are many different normal distributions, with each one depending on two parameters: the population mean, μ, and the population standard deviation, σ. Rather than performing computations on each new set of parameters for a variety of normal curves, it is easier to work in reference to the "simplest case" of the normal curves, called the standard normal distribution.
A parameter is a numerical measurement describing some characteristic of a population. |
 |
|
A standard normal distribution is a special case of the normal distribution. It is a normal distribution with a mean of zero and a standard deviation equal to one. The total area under its density curve is equal to 1. |
|
In a standard normal distribution, the random variable, x, is called a standard score, or a z-score. The horizontal scale of the graph of the standard normal distribution corresponds to z-scores.
All normal distributions are equivalent to the standard normal distribution when the unit of measure is changed to measure standard deviations from the mean. The standard normal distribution can be used to deal with any problem involving any normal distribution. The process of converting a normal distribution into an equivalent standard normal distribution is covered under " Understanding z-scores". 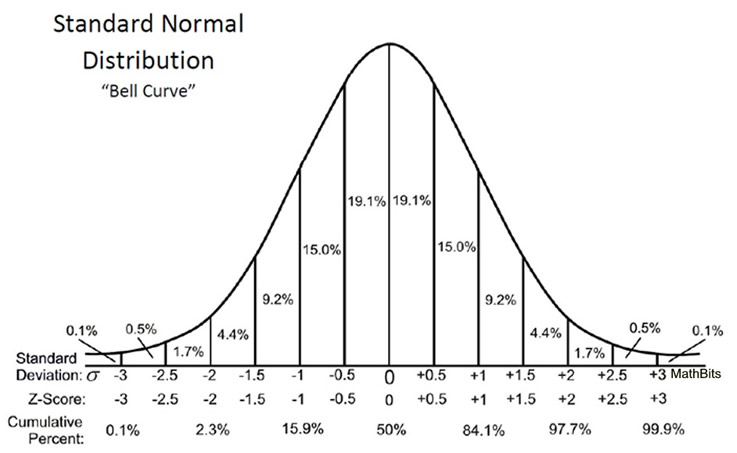
Reading from the chart, it can be seen that approximately 19.1%
of normally distributed data is located between the mean (the peak) and 0.5 standard deviations to the right (or left) of the mean.
This chart shows only percentages that correspond to subdivisions up to one-half of one standard deviation. To find percentages for other subdivisions requires a statistical mathematical table or a graphing calculator. |
| Empirical Rule Still True! |
As seen in the normal curve, the Empirical Rule (68-95-99.7 Rule), states that approximately:
• 68% of the data will fall within one standard deviation of the mean.
• 95% of the data will fall within two standard deviations of the mean.
• 99.7% will fall within three standard deviations of the mean. |
Note: The addition of percentages in the standard normal distribution shown above is slightly different than the Empirical Rule's rounded values. |
50% of the distribution lies within 0.67448 standard deviations of the mean
(that is, "centered about the mean", or "in the middle")
.
If you are asked for the interval about the mean containing 50% of the data, you are actually being asked for the interquartile range, IQR. When working with box plots, the IQR is computed by subtracting the first quartile from the third quartile. In a standard normal distribution (with mean 0 and standard deviation 1), the first and third quartiles are located at -0.67448 and +0.67448 respectively. Thus the interquartile range (IQR) is 1.34896.
In a standard normal distribution: IQR = Q3 - Q1 = 0.67448- (-0.67448) = 1.34896
In ANY normal distribution: IQR = Q3 - Q1 = 0.67448σ - (-0.67448σ) = 1.34896σ
(Interquartile range = 1.34896 x standard deviation)
This will be the population IQR. |

Percentiles
and the Normal Curve |
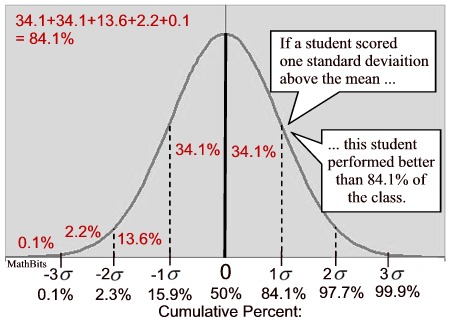
The mean (at the center peak of the curve) is the 50th percentile (50%).
The term "percentile rank" refers to the area (probability) to the left of the value.
Adding the given percentages from the chart will let you find certain percentiles along the curve. |
 |
|