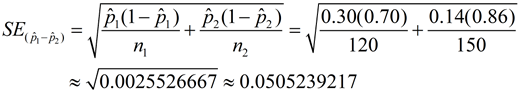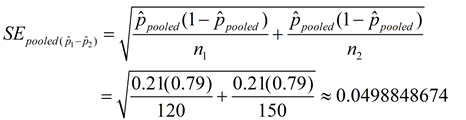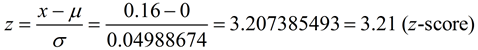|
Up to this point, we have made statistical inferences regarding the proportion, or mean, of a single population. We are now going to look at comparing two population proportions, or means, and examine their differences. We will be looking to determine if the differences are of statistical significance.
 |
Statistical significance means unlikely to occur due only to random sampling. |
|
Consider two groups where one group is comprised of students who studied for a test, and the other group is comprised of students who did not study for the same test. When the test scores are examined, will the test scores of the students who studied be significantly higher? And if the scores are higher, is it due to the studying or is it due to chance?
Null hypothesis: When a study involves drawing samples from two populations, there is always the possibility that any observed statistical difference could occur due to random sampling or sampling error. If this is the case, there may be no significant difference with the statistic being examined in the experiment (the test statistic). The concept of "no difference between the groups' statistics" is referred to as the null hypothesis (H0 ). To do a hypothesis test, we assume the null hypothesis is true, which means that there is no difference between the test statistics (their difference equals zero). We then try to reject (disprove) the null hypothesis. It's sort of like doing an indirect proof in geometry (starting with the opposite of what you hope to be true).
Alternative hypothesis: There is the possibility that the difference between the groups' statistics is due to the treatment given to one group (such as studying). To accept this possibility, and to reject the idea of a null hypothesis, the result of the experiment has to be identified as being statistically significant (unlikely to have occurred due to random sampling alone). The null hypothesis can be rejected if a large enough difference is seen between the two statistics being observed. You must show that the probability of getting results as extreme, or more extreme, than your observed difference is very,very low. The claim that there "IS a difference between the two groups' statistics" is referred to as the alternative hypothesis (H1 ).
Several different techniques, referred to as hypothesis tests, can be used to investigate the differences between group statistics. We will be examining two techniques in our search for the possibility of statistical significance. At this level, we will just be touching the statistical surface on these comparisons.
| First, we will look at a method called Randomization Testing. |
This method is also called the permutation test.
 Comparing Means: Comparing Means: |
A randomization test is a type of statistical significance test. Randomized testing involves using every possible "shuffle" (re-sample) of the data, and the number of re-samples grows astronomically as the sample size increases. Due to the tedious work associated with obtaining all of the re-samples, this test was not widely used and is still not addressed in many newer statistical textbooks. While powerful, the test is easiest used with smaller sets of data when done by hand. The use of computer software to prepare the re-samples has placed the test in a more favorable light.
Consider the number of re-samples needed in these situations:
With 2 cases in each of 2 groups: 4C2 = 6 re-samples.
With 3 cases in each of 2 groups: 6C3 = 20 re-samples.
With 4 cases in each of 2 groups: 8C4 = 70 re-samples.
With 5 cases in each of 2 groups: 10C5 = 252 re-samples.
With 10 cases in each of 2 groups: 20C10 = 184,756 re-samples.
An alternative approach using computer software can be used to randomly re-sample the data thousands of times (1,000, 10,000) and count the number of times the difference is as big, or bigger than, the observed difference. If the number of re-samples is very large, this proportion will be very close to the proportion you would get if you had listed all possible re-samples.
|
Let's follow through a randomization test (done by hand). The amount of our data will be extremely small to allow for ease of demonstration.
| Step 1 |
Identify the hypothesis for this experiment:
Null hypothesis: There is no difference between test scores of those who studied and those who did not study. The mean of the distribution of the mean differences will be the same (or nearly the same) as the experiment's mean difference.
Assume the null hypothesis is true.
Alternative hypothesis: Those who studied will get better (greater) test scores than does who did not study.
(Express the alternative hypothesis as an inequality.)
The experiment's mean difference will be considerably greater than the mean of the distribution of the mean differences. |
Test Scores (out of 100):
Studying |
No Studying |
98 |
60 |
82 |
72 |
Mean = 90 |
Mean = 66 |
This is the experiment's data. |
| Step 2 |
Gather the data for the groups in the experiment, and calculate the difference of the test statistic (in this case, the test statistic being studied is the mean 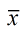 ). ). |
The data is shown above.
The difference in the means is 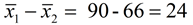 |
| Step 3 |
"Shuffle" (re-sample) the data into all possible situations. Calculate the difference of the means in each case.
The scores can now jump anywhere in the table, since we are working off the null hypothesis that there really is no difference between the test scores.
4C2 = 6 re-samples needed.
|
Studying |
No Studying |
60 |
98 |
82 |
72 |
Mean = 71 |
Mean = 85 |
Difference = -14 |
| |
Studying |
No Studying |
72 |
98 |
82 |
60 |
Mean = 77 |
Mean = 79 |
Difference = -2 |
Studying |
No Studying |
60 |
98 |
72 |
82 |
Mean = 66 |
Mean = 90 |
Difference = -24 |
Studying |
No Studying |
98 |
60 |
72 |
82 |
Mean = 85 |
Mean = 71 |
Difference = 14 |
| |
Studying |
No Studying |
98 |
72 |
60 |
82 |
Mean = 79 |
Mean = 77 |
Difference = 2 |
Create the randomization distribution.
Values of the test statistic are 24, -14, -2, -24, 14, 2
(assuming the null hypothesis is true)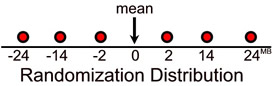 |
| Step 4 |
Compute the probability of getting a difference value as extreme as, or more extreme than, the difference value obtained in the experiment.
Compare the number of entries in the distribution at, or above, 24 with the total number of entries in the distribution. |
There is only one occurrence of 24 in this small distribution (none above). The probability is 1/6 or 0.1666666667 |
| Step 5 |
Examine the size of the probability:
A Very Small Probability: Researchers will establish the "cut off" value for the term "small" before the statistical analysis is prepared. The typical value for "small" is 0.05 or 5%. This value may be smaller depending upon the experiment. If the probability of the difference value from the experiment is less than or equal to 5%, the experiment most likely did not happen by "chance" alone. Thus, the results show a statistically significant difference between the two groups.
In a normal (bell shape) distribution, the 5% is split between the two tails of the graph, keeping the needed value outside of the 2 standard deviations from the mean range.
Not a Very Small Probability: If the probability of the difference value from the experiment is greater than 5%, it is considered not unusual, and it could be typical "chance" behavior. Thus, a statistically significant difference does not exist in this experiment.
|
16.7% is not statistically considered a "small" probability.
Unfortunately, the information from this experiment is being hindered by its small size. The "5% or less" guideline needed for statistical significance cannot be satisfied in this extremely small sample. |
While the example shown above deals with the mean (average) of the data in the experiment,
it is also possible to work with proportions in the experiment.

Now, we will take a look at a method called a Two-Proportion z-Test.
|
This test is more computationally oriented. Grab your calculator.
 Comparing Proportions: Comparing Proportions: |
| With the popularity of the television program "Dancing with the Stars", student researchers decided to investigate the question " Are men, or women, better dancers?" The students randomly asked this question of students in their school with the following results: |
 |
Of 120 male students surveyed, 30% said men are better dancers.
Of 150 female students surveyed, 14% said men are better dancers. |
The students then investigated the data and tried to determine whether the difference in responses was due to a gender gap in opinions as to which sex is the better dancer, or
the difference in responses was due to random sampling variability (chance).

Again, the goal is to determine if this survey uncovered data whose difference will determine statistical significance.
As we saw in the first method, we are looking for the difference value obtained in the survey to be large enough so that the probability of the sampling distribution (of the differences) showing a difference value as extreme, or more extreme, would be very small.
We are going to compare the difference from the survey with the standard deviation of the sampling distribution of the differences.
| Step 1 |
Identify the hypothesis for this experiment:
Null hypothesis: There is no difference between the opinions of men and women regarding whether men or women are better dancers.
We assume that the null hypothesis is true. H0: p1 - p2 = 0
Alternative hypothesis: The percentage of men choosing men as better dancers will be greater than the percentage chosen by women.
We will try to disprove the null hypothesis. H1: p1 - p2 ≠ 0 |
| Step 2 |
Establish the sample proportions:
Sample proportion: 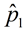 = 30% of 120; 36 out of 120 = 0.30 = 30% of 120; 36 out of 120 = 0.30
Sample proportion: 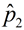 = 14% of 150; 21 out of 150 = 0.14 = 14% of 150; 21 out of 150 = 0.14
Remember, since there are two populations, there are two parameters:
p1 = proportion of male students who chose men as the better dancers
p2 = proportion of female students who chose men as the better dancers |
| Step 3 |
Estimate the difference in the sample proportions:
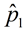 - - 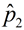 = 0.30 - 0.14 ≈ 0.16 = 0.30 - 0.14 ≈ 0.16 |
| Step 4 |
Establish a sampling distribution of the sample differences:
The mean of this sampling distribution is p1 - p2, or zero (since the null hypothesis is assumed true). |
| Step 5 |
Find the standard deviation (standard error) for the differences of the sample proportions:
From our past work with sampling distributions of sample proportions, we know that when the sample size is large enough (> 30), the sampling distribution is approximately normal, and that the standard error (standard deviation) is 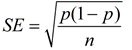 , where p is the mean of the sampling distribution. These facts are true when working with one population.
Since we are dealing with 2 populations (two variables) we expand this concept: , where p is the mean of the sampling distribution. These facts are true when working with one population.
Since we are dealing with 2 populations (two variables) we expand this concept:
The variance of the difference of two independent random variables is the sum of their variances. |
Remember that variance is the square of the standard deviation (or the standard error).
The standard error for the difference of the sample proportions will be:
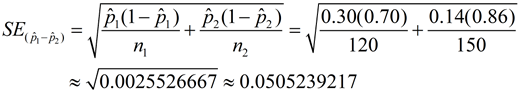
There is a process called "pooling" that can give us a slightly more accurate result when comparing proportions. Since the null hypothesis says that there is no difference between the proportions, it is saying that the proportions are equal (thus dealing with ONE proportion). So, it would be more accurate if the standard error could also deal with only one proportion.
The solution to obtaining only one proportion is to "pool" the proportions together.
According to the null hypothesis, both groups have the same proportion, since
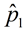 - - 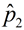 = 0. Overall,
36 + 21 = 57 out of a total of 120 + 150 = 270 students that chose men as better dancers. That proportion is 57/270 = 0.2111111111. Now, compute the standard error formula using this "pooled" proportion in place of = 0. Overall,
36 + 21 = 57 out of a total of 120 + 150 = 270 students that chose men as better dancers. That proportion is 57/270 = 0.2111111111. Now, compute the standard error formula using this "pooled" proportion in place of  and and  . .
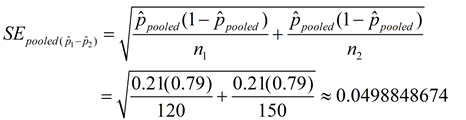
|
| Step 6 |
Determine if there is statistical significance:
To determine whether a result is statistically significant, a researcher sets the probability of rejecting the null hypothesis at 0.05 or 5%. This basically means that the rejection region consists of 5% of the sampling distribution. Since the graph of the sampling distribution is approximately normal, the 5% is partitioned to both sides of the distribution with each rejection region containing 2.5% of the distribution. This will be more (or less) than 2 standard deviations (95%).
So, how do we decide if the difference we see, 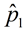 - - 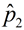 , is "large" enough to give us statistical significance? , is "large" enough to give us statistical significance?
We compare the difference with the standard error. Since the sampling distribution (based upon the null hypothesis that the difference is 0) is Normal, we can divide the observed difference by the standard error to get a z-score.
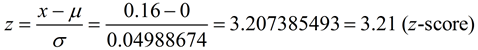
The z-score will tell how many standard errors the difference is from 0. Since we are looking at a cut-off of 5%, this value will need to be greater (or less) than 2 standard deviations (or standard errors) from 0.
Standard error is an estimate of the standard deviation of a statistic.
Assuming the null hypothesis to be true, we would expect the sampling distribution of the sample differences to be approximately a normal curve about the mean of 0.
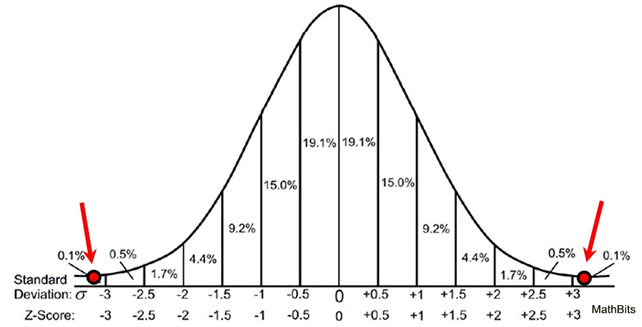
The z-score (3.21) shows that our experimental difference is beyond 2.5 standard deviations above the mean. This puts our observed value into the 2.5% of the distribution signifying statistical significance for our difference.
From the z-Table, we get a "probability/area to the left of the value 3.21" to be 0.9993. So to the right of this value, we have 1 - 0.9993 = 0.0007. Allowing also for the possibility of a negative difference result, we get a probability (called a p-value) of 2(0.0007) = 0.0014.
Conclusion: The p-value of 0.0014 tells us that if the null hypothesis is true (no differences between the proportions), then the difference observed in this study would happen only 14 times in 10,000. This is rare enough for us to conclude that there IS a difference in the gender opinions regarding whether men or women are better dancers. It appears that men are more likely to feel that men are better dancers. |
In hypothesis testing, certain conditions must be met before testing.
1. It is assumed that the data values are independent from each other. The data values cannot affect one another.
2. The data must be sampled at random or generated from a properly randomized experiment.
3. The sample size should not exceed 10% of the population. Samples are almost always drawn without replacement. If the sample exceeds 10% of the population, the probability of a success changes so much during sampling that a Normal model may no longer be appropriate.
4. The sample size must be large enough to make the sampling model for the sampling proportions approximately Normal. We must expect at least 10 "successes" and at least 10 "failures" in the sample data.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|



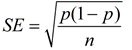 , where p is the mean of the sampling distribution. These facts are true when working with one population.
Since we are dealing with 2 populations (two variables) we expand this concept:
, where p is the mean of the sampling distribution. These facts are true when working with one population.
Since we are dealing with 2 populations (two variables) we expand this concept: