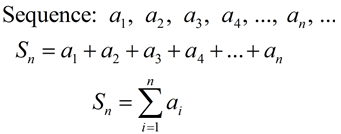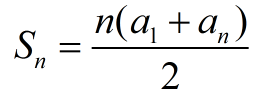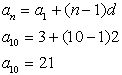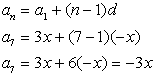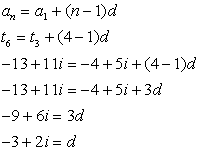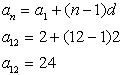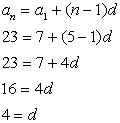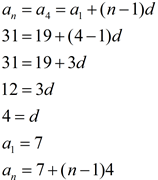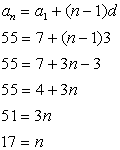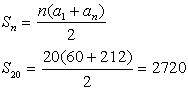|
Some sequences are composed of simply random values, while others have a definite pattern that is used to arrive at the sequence's terms. The arithmetic sequence (or progression), for example, is based upon the addition of a constant value to arrive at the next term in the sequence.
Arithmetic Sequences |
 Add
Add |
|
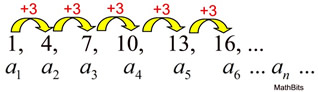
Arithmetic sequences follow a pattern of adding a fixed amount from one term to the next. The number being added to each term is constant (always the same).
a1, (a1 + d), (a1 + 2d), (a1 + 3d), ...
The fixed amount is called the common difference, d, referring to the fact that the difference between two successive terms yields the constant value that was added. To find the common difference, subtract the first term from the second term. |
|
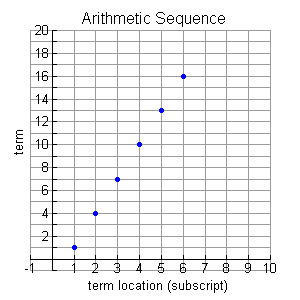
Arithmetic sequences have a linear nature when graphed (as a scatter plot). The domain consists of the counting numbers 1, 2, 3, 4, ... (representing the location of each term) and the range consists of the actual terms of the sequence. In the graph shown above, while the x-axis increases by a constant value of one, the y value increases by a constant value of 3.
 Arithmetic Sequences Arithmetic Sequences
| Arithmetic Sequence: |
Common Difference, d: |
1, 6, 11, 16, 21, 26, ... |
d = 5. A 5 is added to each term to arrive at the next term.
OR ... the difference a2 - a1 = 5. |
10, 8, 6, 4, 2, 0, -2, -4, ... |
d = -2. A -2 is added to each term to arrive at the next term.
OR ... the difference a2 - a1 = -2. |
|
d = -½. A -½ is added to each term to arrive at the next term.
OR ... the difference a2 - a1 = -½. |

Arithmetic Series |
 Summation
Summation |
|
When the terms of a sequence are added together, the sum is referred to as a series. We will be working with finite sums (the sum of a specific number of terms). |
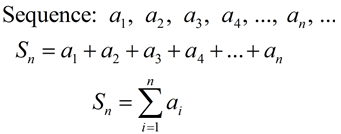 This is the sum of the first n terms.
This is the sum of the first n terms. |
Arithmetic Series: Sn = a1 + (a1 + d) + (a1 + 2d) + (a1 + 3d) + ... + (a1 + (n - 1)d)
An arithmetic series is the adding together of the terms of an arithmetic sequence.

 Formulas used with arithmetic sequences and arithmetic series: Formulas used with arithmetic sequences and arithmetic series:
To find any term
of an arithmetic sequence:
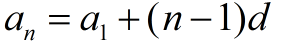
where a1 is the first term of the sequence,
d is the common difference,
n is the number of the term to find. |
Note: you may see a1 simply referred to as a. |
To find the sum of a certain number of terms of an arithmetic sequence:
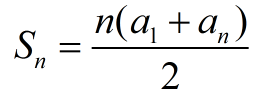
where Sn is the sum of n terms ( nth partial sum),
a1 is the first term, an is the nth term. |
Note: (a1 + an)/2 is the mean (average) of the first and last terms. The sum can be thought of as the number of terms times the average of the first and last terms.
This formula may also appear as 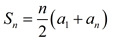 |
Click here to see "How these Formulas were Created". |

Let's take a look at a variety of examples working with arithmetic sequences and series.
Read the "Answers" carefully to find "hints" as to how to deal with these questions.

Questions:
|
Answers: |
1. Find the common difference for this arithmetic sequence: 4, 15, 26, 37, ... |
The common difference, d, can be found by subtracting the first term from the second term, which in this example yields 11. Checking shows that 11 is the difference between all of the terms. |
2. Find the common difference for the arithmetic sequence whose formula is:
an = 6n + 3. |
A listing of the terms will show what is happening in the sequence (start with n = 1). 9, 15, 21, 26, 33, ...
The common difference is 6. |
3. Find the 10th term of the sequence:
3, 5, 7, 9, 11, ... |
By observation: n = 10, a1 = 3, d = 2
Use the formula for the nth term.
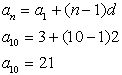
The 10 th term is 21.
|
4. Find a7 for an arithmetic sequence where:
a1 = 3x and d = -x . |
By observation: n = 7, a1 = 3 x, d = - x
Your answer will be in terms of x.
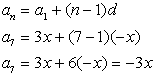
|
5. Given the arithmetic sequence:
f (1) = 4; f (n) = f (n - 1) + 3. Find f (5). |
Don't let the change to functional notation distract you. This problem shows recursive form: each term is defined by the term immediately in front of it.
The first term is 4 and the common difference is 3. Since we only need the fifth term, we can get the answer by observation:
4, 7, 10, 13, 16 f (5) = 16 |
6. Find t15 for an arithmetic sequence where:
t3 = -4 + 5i and t6 = -13 + 11i
NOTE: Using
high subscript - low subscript + 1
will count the number of terms. |
|
Notice the change of labeling from a to t. The letter used in labeling is of no importance. Let's get a visual of this problem.  Using the third terms as the "first" term, find the common difference from these known terms.
Using the third terms as the "first" term, find the common difference from these known terms.
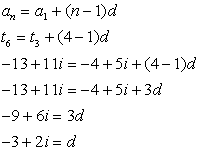
Now, from t3 to t15 is 13 terms.
t15 = -4 + 5 i + (13-1)(-3 +2 i) = -4 + 5 i -36 +24 i
= -40 + 29 i |
7. Find an explicit formula and a recursive formula for the sequence:
1, 3, 5, 7, 9, ... |
The explicit formula needs to relate the subscript number of each term to the actual value of the term. These terms are odd numbers
(a good formula pattern to remember).
an = 2n - 1
Substituting n = 1 gives 1.
Substitution n = 2 gives 3, and so on.
The recursive formula, where each term is based upon the term immediately in front of it, is easy to find since the common difference is 2.
a1 = 1
an = an-1 + 2.
|
8. The first three terms of an arithmetic sequence are represented by x + 5, 3x + 2, and 4x + 3 respectively. Find the numerical value of the 10th term of this sequence. |
Represent the common difference between the terms:
(3x + 2) - (x + 5) = 2x - 3 (the common difference)
(4x + 3) - (3x + 2) = x + 1 (the common difference)
Since the common difference must be constant, we set these values equal and solve for x.
2x - 3 = x + 1
x = 4
The sequence is 9, 14, 19, ...,
common difference of 5.
The 10th term = 9 + (10 - 1)(5) =
54
|
9. Find the sum of the first 12 positive even integers.
Notice how
BOTH formulas
work together to arrive
at the answer. |
|
The word "sum" indicates the need for the sum formula.
positive even integers: 2, 4, 6, 8, ...
n = 12, a1 = 2, d = 2
We are missing a12, for the sum formula, so we use the "any term" formula to find it.
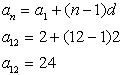 Now, we use this information to find the sum:
Now, we use this information to find the sum:
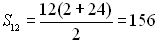 |
10. Insert 3 arithmetic means between 7 and 23.
Note: In this context, an arithmetic mean is the term between any two terms of an arithmetic sequence. It is simply the average (mean) of its surrounding terms. |
|
While there are several solution methods, we will use our arithmetic sequence formulas.
Draw a picture to better understand the situation.
7, ___, ___, ___, 23
This set of terms is an arithmetic sequence.
We know the first term, a1, the last term, an, but not the common difference, d. This question gives NO indication of "sum", so avoid that formula.
Find the common difference:
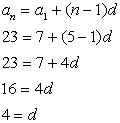
Now, insert the terms using d:
7, 11, 15, 18, 23 |
11. In an arithmetic sequence, a4 = 19 and
a7 = 31. Determine the formula for an, the nth term of this sequence.
|
Visualize the problem by modeling the terms from the fourth to the seventh.
19, _____. _____, 31
Temporarily imagine that 19 is the first term. This will allow us to find the common difference.
Imagined Observations:
a1 = 19, a4 = 31, n = 4.
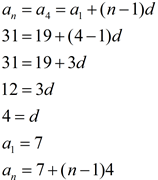
|
12. Find the number of terms in the sequence:
7, 10, 13, ..., 55
Note: n must be an integer! |
|
By observation: a1 = 7, an = 55, d = 3.
We need to find n. This question makes No mention of "sum", so avoid that formula.
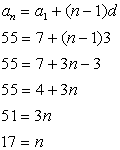
When solving for n, be sure your answer is a positive integer. There is no such thing as a fractional number of terms in a sequence! |
13. A theater has 60 seats in the first row, 68 seats in the second row, 76 seats in the third row, and so on in the same increasing pattern. If the theater has 20 rows of seats, how many seats are in the theater? |
The seating pattern is forming an arithmetic sequence:
60, 68, 76, ...
We need to find the "sum" of all of the seats.
By observation: n = 20, a1 = 60, d = 8 and we need a20 for the sum.
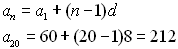
Now, use the sum formula.
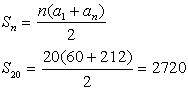
There are 2720 seats. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|