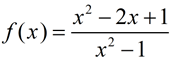|
Directions: The following questions pertain to graphs of rational functions.
Do not use your graphing calculator, unless instructed to do so.
1. |
At what x-value location(s) would you find vertical asymptotes for the function 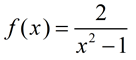 ? |
|
|
2. |
Given the function  :
|
a) What is the x-intercept of this graph?
Choose:
|
b) What is the equation of the vertical asymptote?
Choose:
|
|
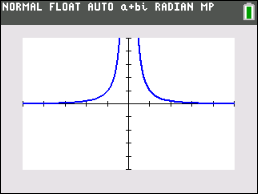
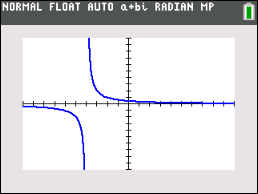
3. |
Given the graph shown at the right in a 10 x10 viewing window. Which of the following equations could have possibly been used to produce this graph?
(Do not use your graphing calculator!) |
|
Choose:
|
|
4. |
Which of the following functions has x = 0 as a vertical asymptote?
(Do not use your graphing calculator!)
|
|
|
5. |
The characteristics of the following function are that its zeros are at x = -1 and x = 3 and its vertical asymptote is at x = 0. 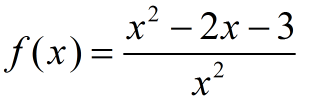
|
|
|
|
6. |
Which of these functions has no vertical asymptotes?
(Check this one out on your graphing calculator.)
|
|
|
7. |
Given the graph of 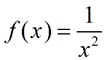 shown at the right. Which of the following statements describes the behavior of the graph as x approaches positive infinity? |
|
|
|
8. |
Find the x-intercept for the function:
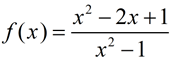
(Do not use your graphing calculator!)
|
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|

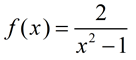 ?
?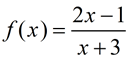 :
:
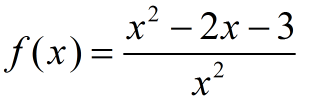

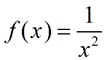 shown at the right. Which of the following statements describes the behavior of the graph as x approaches positive infinity?
shown at the right. Which of the following statements describes the behavior of the graph as x approaches positive infinity?