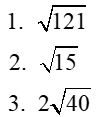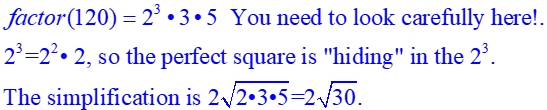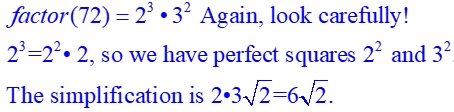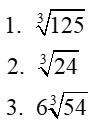Our calculator work in Algebra 2 will be focused primarily on the TI-Nspire CX II (non CAS).
(The CAS version will be utilized in PreCalculus and Calculus.)
Go to Finding Your Way Around the TI-Nspire Graphing Calculator for more help.

Simplifying Square Roots

The TI-Nspire CX II (non-CAS) will give you a numerical approximation for a square root, but it will not express the square root in simplified radical form (assuming the square root to not be a perfect square.)

Numerical Approximation:
(or exact value when dealing with a perfect square)

Remember you can access the radial symbol under
the symbol .


The calculator can, however, "help" you to determine if the square root CAN be simplified, and how to develop the simplification. Let's take a look at what can be done.

Calculator "HELP" for simplifying:

The calculator can "help" when simplifying a square root, by examining the factorization of the radicand (number under the radical).

The objective is to look for factors that create perfect squares and use them to create the number in front of the square root symbol. Thus, you are taking the square roots of the perfect squares.
Keystrokes:           #2 Number     #3 Factor   

  

Note: When we get to using the TI-NSpire CX II CAS, that calculator will be capable
of giving you the simplified radical in radical form.


Use Calculator to CHECK your work

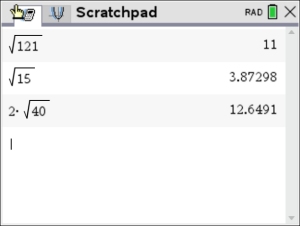
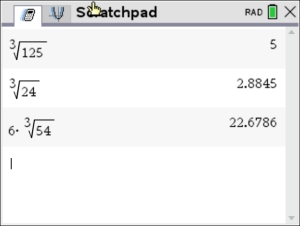
If you simplified your radical by hand, let's check your answer on the calculator. Type the question and the answer as being equal and see if the calculator tells you the result is TRUE (meaning your simplification is correct)!

BUT ...

Notice the 4th entry WARNING! The entry is TRUE, but the calculator is saying FALSE. The calculator will display a pop-up that says "Result obtained using approximate arithmetic."

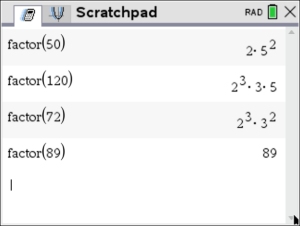
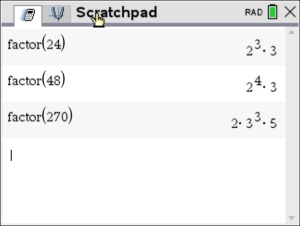
So, if you are using this "equation" strateg for checking, and you get a "false" result, look further. Try typing each entry separately and check assigned decimal values. Place the calculator setting on FLOAT to get largest possible decimal result.
This can be problematic, so be careful.

If each side of the equation is entered separately, there appears to be no problem out to 10 decimal places.


Why is this "Warring" happening? The TI-NSpire (not CAS) uses what is called "floating-point arithmetic" to compare "approximate arithmetic" results: which can sometimes be problematic, especially when dealing with irrational numbers. Because the calculator is dealing with non-ending decimal values, there are bound to be rounding and precision limitations, and potential errors.

Note: When we get to using the TI-NSpire CX II CAS, that calculator will be capable
of giving exact answer in radical form, avoiding this problem.

 

Cube Root Function



Th calculator will also yield numerical approximations when working with cube roots.

Getting numerical results:


The same factorization stategy can also work for simplifying cube roots.
The difference is that this time you will be looking for perfect cubes instead of perfect squares.

Calculator HELP for simplifying:

The calculator can help when simplifying a cube root, by examining the factorization of the radicand (number under the radical).

The objective is to look for factors that create perfect cubes and use them to create the number in front of the cube root symbol. Thus, you are taking the cube root of the perfect cubes.
Keystrokes:           #2 Number     #3 Factor   


For
calculator help with radical expressions.
click here.
For
calculator help with mode settings.
click here.
Graphing Radicals Mode Settings
 

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".
Radical Expressions