| This section will take a look at dividing radical expressions including work with variables. (Assume variables to be positive, real numbers.) |
 Dividing
Dividing |
When dividing radicals (with the same index), divide under the radicals, and then divide any values directly in front of the radicals. |
|
REMEMBER:
A conjugate is a binomial formed by negating the second term.
Example: the conjugate of (x + y) is (x - y).

|
|
Quotient Rule
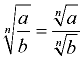
where a ≥ 0, b > 0
"The radical of a quotient is equal to the quotient of the radicals of the numerator and denominator."
|
|
|
|
ANSWER: 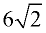 |
| |
Divide out front and divide under the radicals. 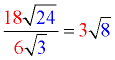
Then simplify the result. 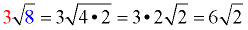
Yes, you could also have started by simplifying the squarer root of 24.
|
|
|
ANSWER: 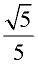 |
| |
This fraction will be in simplified form when the radical is removed from the denominator. If we create a perfect square under the square root radical in the denominator, the radical can be removed. To do so, we multiply the top and bottom of the fraction by the same value (this will create multiplying by "1"). If we multiply by the same square root that we are trying to remove (in this case multiply by 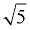 ), the radicand will be a perfect square, which will remove the square root from the denominator. ), the radicand will be a perfect square, which will remove the square root from the denominator.
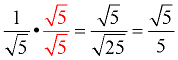 You have just "rationalized" the denominator"! You have just "rationalized" the denominator"!
You turned an irrational value into a rational value in the denominator.
|
 |
 |
ANSWER: 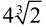 |
| |
We need to "rationalize the denominator for a cube root". When the denominator is a cube root, you have to work harder to get it out of the bottom. Unfortunately, it is not as easy as choosing to multiply top and bottom by the radical, as we did in Example 2 with the square root. Here is why:
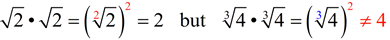
In the first case, the power of 2 and the index of 2 allow for a perfect square under a square root, and the radical can be removed by the inverse property.
In the second case, the power of 2 with an index of 3 does not create an inverse situation and the radical is not removed. We need an additional factor of the cube root of 4 to create a power of 3 for the index of 3.
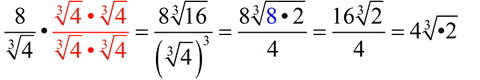
It may be the case that the radicand of the cube root is simple enough to allow you to "see" two parts of a perfect cube hiding inside. In this case, you can simplify your work and multiply by only one additional cube root. As shown below, one additional factor of the cube root of 2, creates a perfect cube in the radicand.
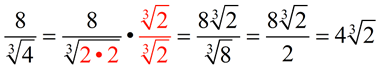
|
 |
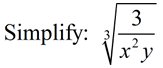 |
ANSWER: 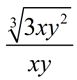 |
| |
Using the approach we saw in Example 3 above, we multiply by two additional factors of the denominator. Look for perfect cubes in the radicand as you multiply to get the final result. The purpose is to rationalize the denominator.
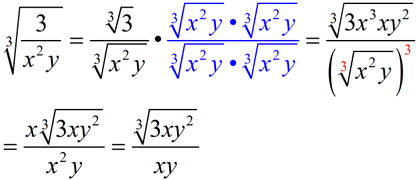
Or, another approach is to create the simplest perfect cube under the radical in the denominator.
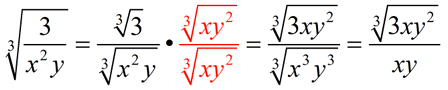
|
 |
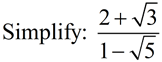 |
ANSWER: 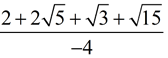 |
| |
We will use a conjugate to rationalize the denominator! The problem with this fraction is that the denominator contains a radical. As such, the fraction is not considered to be in simplest form. As we saw in the last section, multiplying a binomial times its conjugate will rationalize the product. This process will remove the radical from the denominator in this problem ( if we multiply the denominator by 1 + 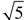 ). So as not to "change" the value of the fraction, we will multiply both the top and the bottom by 1 + ). So as not to "change" the value of the fraction, we will multiply both the top and the bottom by 1 + 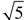 , thus multiplying by 1. , thus multiplying by 1.
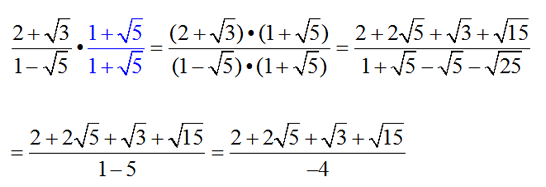
While the numerator "looks" worse, the denominator is now a rational number and the fraction is deemed in simplest form. Notice that there is nothing further we can do to simplify the numerator.
Did you notice how the process of "rationalizing the denominator" by using a conjugate resembles the "difference of squares": a2 - b2 = (a + b)(a - b)? They both create perfect squares, and eliminate any "middle" terms.
|
 |
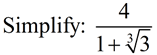 |
ANSWER: 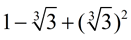 |
|
While the conjugate proved useful in the last problem, when dealing with a square root in the denominator, it is not going to be helpful with a cube root in the denominator. Watch what happens when we multiply by a conjugate:
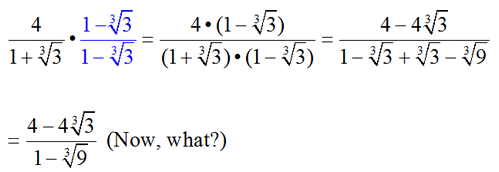
The cube root of 9 is not a perfect cube and cannot be removed from the denominator. Instead of removing the cube root from the denominator, the conjugate simply created a new cube root in the denominator.
To solve this problem, we need to think about the "sum of cubes formula":
a3 + b3 = (a + b)(a2 - ab + b2). This formula shows us that to obtain perfect cubes we need to multiply by more than just a conjugate term.
Let a = 1 and b = the cube root of 3. We will multiply top and bottom by
a2 - ab + b2.
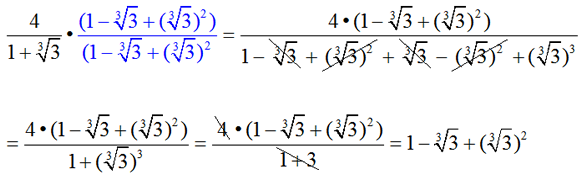
WOW!
Note: If the denominator in this problem had been 1 "minus" the cube root of 3, the "difference of cubes formula" would have been used:
a3 - b3 = (a - b)(a2 + ab + b2).
|
|
|