small logo
Radical Arithmetic: Add, Subtract,
Multiply including Variables
MathBitsNotebook.com

Topical Outline | Algebra 2 Outline | MathBits' Teacher Resources

Terms of Use   Contact Person: Donna Roberts
divider
Adding and Subtracting

This section will take a look at adding and subtracting radical expressions including work with variables. (Assume variables to be positive, real numbers.)

statement
Add/Subtract
Adding and subtracting radicals: For radicals having the same index and the same values under the radical (the radicands), add (or subtract) the values in front of the radicals and keep the radical.

bulletREMEMBER: Always simplify first! When the radicals in an addition or subtraction problem are different, be sure to check to see if the radicals can be simplified. It may be the case that when the radicals are simplified, they will become "like" radicals, making it possible for them to be added or subtracted.


expin1
as1
ANSWER: as2
 

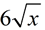Since the radicands are the same, add and subtract the coefficients (the numbers in front of the radicals).
ex2
radas6
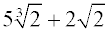ANSWER: radas6ab
 
Notice that this problem mixes cube roots with a square root.
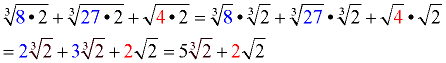
radas6a

beware
You cannot combine cube roots with square roots when adding.
They are not "like radicals".

 
ex3 as3
 ANSWER: as5
 

Simplify each term first. Then see if the expressions can be added.as4
Simplifying showed that we actually had similar radicals which could be added.
ex1 as7 ANSWER: as8
  Simplify first.
radnew2
Each term simplified to show similar radicals which could be subtracted.

Multiplying

This section will take a look at multiplying radical expressions
including expressions containing variables.

statement
Multiplying
When multiplying radicals (with the same index), multiply under the radicals, and then multiply any values directly in front of the radicals.
Product Rule
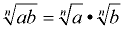rule n multwhere a ≥ 0, b≥ 0

"The radical of a product is equal to the product of the radicals of each factor."
expin1
mu math2
ANSWER: mu math2c
 

Multiply out front and multiply under the radicals. mu math2a
Then simplify the result.
mu math 2b
ex2
mu math3
ANSWER: mu math3c
 
Multiply under the radicals. mm3aa
Then simplify the result.
mu math3b

 
ex2 mdv1 ANSWER:    6x2
  Multiplying will yield two perfect squares.
mdv2
ex2 mdv3 ANSWER: mdv17
 

Search out the perfect cubes and reduce. This will simplify the multiplication. If you do not "see" the perfect cubes, multiply through and then reduce.
mdv16

 
ex2 mdv4 ANSWER: mdv7
 

In this problem, it is easier to reduce the radicals before multiplying since the perfect cube (27) can be more clearly seen in each radicand. Yes, you could have chosen, instead, to multiply and then reduce.
mdv5
ex2 mu math4 ANSWER: mu math4c
 

Distribute across the parentheses. Remember there is an implied "1" in front of 4aa.
mu math4a
Then simplify the result. mu math4b

 
ex2 d ANSWER: radex5c
 

Use the distributive property to multiply. Combine like terms.
radex5a

 
ex2 radex6 ANSWER: dnranex6aans
 

Use the distributive property to multiply. There are NO like terms to be combined.
dmradex6a
tidbit
A conjugate is a binomial formed by negating the second term of a binomial.
Example: the conjugate of (x + y) is (x - y).
radconjugate

ex2 md1 ANSWER: x2 - 3
 

These terms are conjugates involving a radical. As with all conjugates, when multiplied, the middle terms cancel each other out. Notice the squaring of the square root. Notice that when the conjugates were multiplied, the radicals disappeared!
md2

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".