Practice Page

Directions: Read carefully.

1.
If the graph shown at the right is a transformation of the parent function 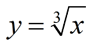crpm1, which choice is a possible equation for this function?
Choose:
crpm3
crp2m
crpm4
crpm5
CRP1

 

 

2.
If the graph shown at the right is a transformation of the parent function 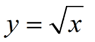crpm1, which choice is a possible equation for this function?
Choose:
crpm7
crpm8
crpm9
crpm10
crp2

 

 

3.
What is the domain of this function?

Choose:
(-4,∞)
(0,∞)
[-4,∞)
[4,∞)
crp2

 

 

4.
Function h(x) is a transformation of function f (x). The function h(x) can be expressed as:

Choose:
h(x) = f (x) - 4
h(x) = f (x - 2) - 4
h(x) = f (x + 2) - 4
h(x) = f (x - 3) - 4
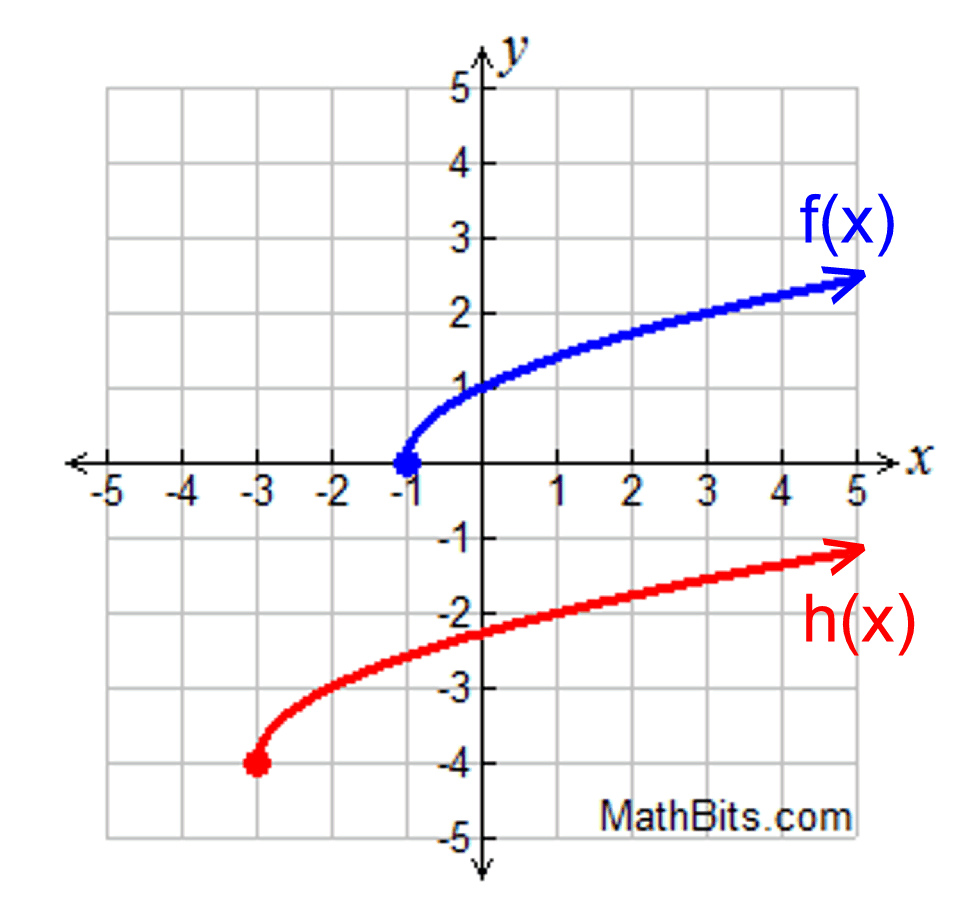crpgraph7a

 

 

5.
Regarding the graph at the right: 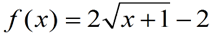crpm11
a) Which interval is the domain?
 Choose:
[-2, ∞)
(0, ∞)
[-1, ∞)
[-2, 0)

b) Which interval is the range?
 Choose:
[-2, ∞)
(0, ∞)
[-1, ∞)
[-2, 0)
crpgraph8
 
 

c) On which interval is the function positive?
 Choose:
[-2, ∞)
(0, ∞)
[-1, ∞)
[-1, 0)
 

d) On which interval is the function negative?
 Choose:
[-2, ∞)
[-1, ∞)
[-2, 0]
[-1, 0)
 

e) Which choice is an end behavior for this function?
 Choose:
As x → ∞, f (x) → 3.
As x → -1, f (x) → -1.
As x → ∞, f (x) → -2.
As x → -1, f (x) → -2.

 

 

6.
Function g(x) is a transformation of the cube root function.
gx

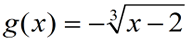
On which interval is the function decreasing?
 Choose:
(-∞,0)
(-∞,2)
(-∞,∞)
(2,∞)
crpgraph9

 

 

7.
Regarding the graph at the right:
f (x) is a transformation of the square root function.
a) What is the domain of f (x)?
 Choose:
[1, ∞)
(-∞, 1]
(-∞, 3]
[3, ∞)

b) Which interval is the range?
 Choose:
(1, ∞)
[1, ∞)
[3, ∞)
(-∞, 3)
pp9
 
 

c) Which of the following statements is true for f (x)?
 Choose:
Increasing and positive on the interval (-∞, 3).
Decreasing and positive on the interval (-∞,3).
Increasing and negative on the interval (-∞,3).
Decreasing and negative on the interval (-∞,3).
 

d) Which choice is a possible equation for f (x)?
 Choose:
eq1
eq3
eeq2
eq4

 

 

8.
Regarding the graph at the right:
h(x) is a transformation of the cube root function.
a) Which interval is the domain?
 Choose:
[0, 4]
[-5, 5]
[0, ∞)
(-∞, ∞)

b) Which point is the x-intercept?
 Choose:
(0,-5)
(0, 2)
(-5, 0)
(2, 0)
pp10
hcube
 
 

c) On which interval is the function positive?
 Choose:
(-∞, ∞)
(-5, ∞)
(2, ∞)
(0, ∞)



divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".