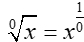Radical and Exponent Relationship
radicalparats
We know that if we square the square root of 3, the result will be simply the radicand 3.
Squaring the square root of the number 3 will leave just the number 3.

"Matching" radicals and exponents are inverse operations.


repic3
repic1

The solution to each radical, when raised to the radical's index, gives the radicand.
Symbolically, we have:  

Applying this relationship, as shown below, we can arrive at the conclusion
that a radical of index "n" raised to a power of "n", will return the radicand "a".

Radical functions and power functions can be inverses of one another.

 

Radicals and fractional (rational) exponents:
repic6

The denominator of the fractional exponent will be the index of the radical.


If n is a positive integer that is greater than 1 and a is a real number, then
infodef

When a is nonnegative, n can be any index.
When a is negative, n must be odd.
For work in this unit, you may assume, unless otherwise directed, that all variables in radicands ("a")
represent non-negative real numbers and that the radicand is non-negative.


When dealing with radicals, it may be advantageous to rewrite the radical using a fractional exponent. The power rules associated with exponents often make the radical computations or simplifications easier.
Note: We can also say: infon

See more about fractional exponents at Fractional (Rational) Exponents.

 

Does the index in a radical "have to be" an integer?


 

Now that we understand the relationship between radicals and rational exponents, we can examine the answers to some perplexing questions about radicals. Consider this example:

You are given the equation p = 14m0.25 and asked to express m in terms of p.
Is 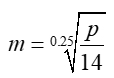an acceptable answer?

In other words, can the index of a radical be a fraction (or decimal)?

The answer is "traditionally" NO.
But "technically" YES.

In past math courses, we have seen the use of radicals indicating that the index must be a positive integer (> 1). This is what is known mathematically as the "standard form of a radical".

Remember, the index of a radical expression indicates the number of times, n. that a specific value is used as a factor to obtain the radicand (the number under the radical, R).
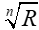is considered the "nth root of the number R".

It is simply "nicer" to have the index be a "counting" number, starting with 2.
(Remember: stay with this traditional definition unless told otherwise by your teacher.)


BUT ... technically the index can also be a fraction (or decimal).

Now, that we understand the relationship between radicals and rational exponents,
we can determine why this is true and how it relates to a fractional exponent.

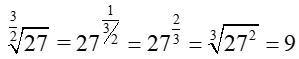
The reciprocal of the fractional exponent is used.
It is simply another way to look at a concept, but it is not "standard radical form".

NOTE: The calculator thinks a fractional index is acceptable.

Side notes:
• How about a negative index? This will deal with the reciprocal of the fractional exponent.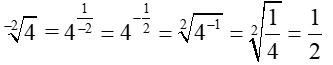
While this is possible, it is not considered to be a "standard radical expression".

• How about a zero index? Now, we have a problem. A zero index is NOT possible since it allows for division by zero:
divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".