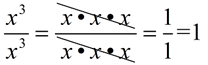
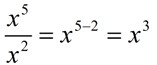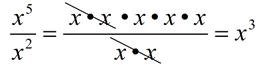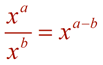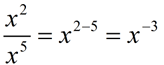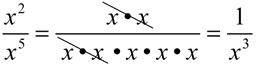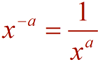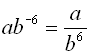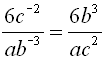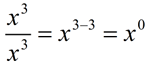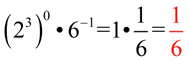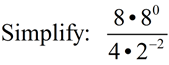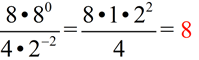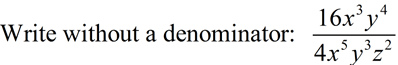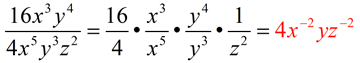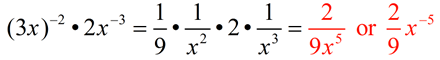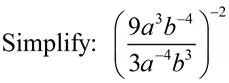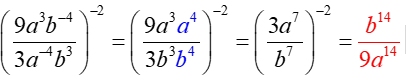From having worked with the rules of exponents (when x is not 0), we know: When the value of a is larger than the value of b, we arrive at the rule for a positive exponent.
When the value of a is smaller than the value of b, we arrive at the rule for a negative exponent.
Should the values of a and b be the same, we have the rule for a zero exponent.
Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|
||||||||||||||||||||||||||||||||||||||||||||||||||