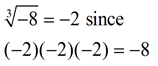|
|
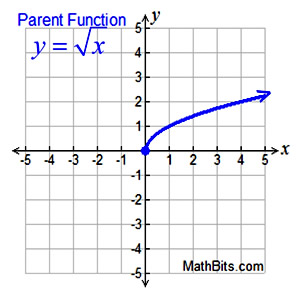
We saw the basics of graphing the "square root" function in Algebra 1.
On this page, we will expand upon those concepts and investigate other radical functions.
Transformations will be discussed at Dealing with Transformation of Radical Graphs.
|
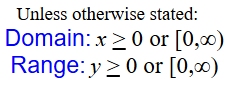
These values are the domain and range
of the parent function.
Remember, a negative value under the radical symbol (the radicand) will not yield a Real number. Thus, the parent domain is limited to numbers greater than or equal to zero.
|
 |

In our numerical and algebraic work with radicals,
we saw that "taking the square root is an "inverse operation" of squaring."
But when we try to directly apply this square root concept of "inverse operations"
to "graphs of functions", we have a small problem.
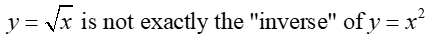
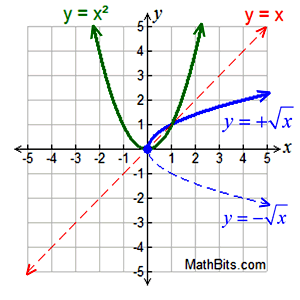
The graph of an inverse "relation" is the reflection of the original graph over the identity line y = x.
(Note: not all inverse graphs are functions.)
The "squaring" function, y = x2, (a parabola) when reflected over the line y = x, produces a side-ways parabola (which is not a function). It can be seen that the positive square root function is only "part" of the inverse of y = x².
Since the square root function cannot have a negative under the radical symbol, the domain of the parent square root function must be limited to the domain [0,∞), to achieve a representative inverse. |
 |

|
Properties:
• square root parent function, 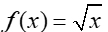
• zero of the function is at (0,0)
• domain is x > 0, or [0, ∞) (interval notation).
• range is [0, ∞)
• x-intercept = y-intercept = (0,0)
• graph is increasing from left to right across the domain, [0,∞), with all y-values being positive (or zero)
• no relative maximum or relative minimum
• no absolute maximum (graph → ∞)
• absolute minimum 0
• end behavior of the parent square root function:
as x → +∞, f (x)
→ +∞,
as x → 0+, f (x)
→ 0,
(coming from the right) |
Square Root Function 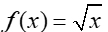
Keep in mind that a square root function will not have a negative number under the radical symbol.
| x |
0 |
1 |
4 |
9 |
16 |
| f (x) |
0 |
1 |
2 |
3 |
4 |
When graphing by hand, choose x-values that yield integer results. Choosing perfect square values for x will be the easiest choices. |
|

|
Negation of the Parent Function. 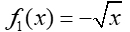
Properties:
• zero, domain, x-intercept, y-intercept, relative max/min, and absolute max/min remain the same.
• range is all non-positive real numbers
• graph is decreasing from left to right across the domain, [0, ∞), with all y-values being negative (or zero).
• end behavior of this negation of the square root function:
as x → +∞, f (x)
→ -∞,
as x → 0+, f (x)
→ 0. (coming from the right)
|
Negation of Square Root Function
 | |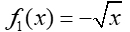
| x |
0 |
1 |
4 |
9 |
16 |
| f1(x) |
0 |
-1 |
-2 |
-3 |
-4 |
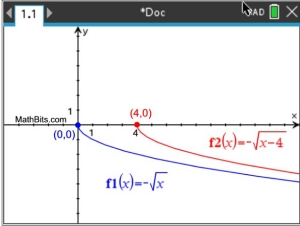
This negation graph is a reflection of the parent function over the x-axis. |
The graph of 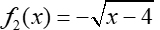 of a transformation also appears on the graph above. of a transformation also appears on the graph above.
This graph is the reflection of the parent function over the x-axis, along with a horizontal shift (translation)
4 units to the right.
The end behavior: as x → +∞, f (x)
→ -∞ and as x → 4+, f (x)
→ 0, |
For a discussion of end behavior in radical functions, see Dealing with End Behavior. |

|
Unless otherwise stated:
Domain: All Reals or (-∞. ∞ ).
Range: All reals or (-∞. ∞ ).
Remember, a negative value under the radical symbol (the radicand) will not be a problem with cube roots.
This function needs no special attention
for "end behaviors". |
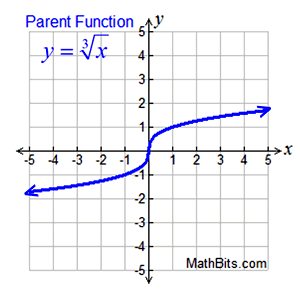 |

Properties:
• cube root parent function, 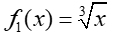 . .
• zero of the function is at (0,0)
• domain is all real numbers, or (-∞, ∞)
• range is all real numbers, (-∞, ∞)
• x-intercept = y-intercept = (0,0)
• graph is increasing from left to right across the domain.
• graph is negative on (-∞. 0) and positive on (0,+∞).
Zero is technically neither positive nor negative.
• no relative maximum or relative minimum
• no absolute maximum (graph → ∞)
• absolute minimum (graph → -∞)
• end behavior of this cube root function:
as x→ +∞, f (x)
→ +∞
as x → -∞, f (x)
→ -∞ |
Cube Root Function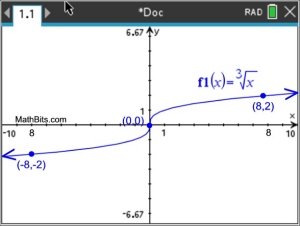
| x |
-8 |
1 |
0 |
1 |
8 |
| f1(x) |
-2 |
-1 |
0 |
1 |
2 |
When graphing by hand, choose x-values that yield integer results. Choose perfect cube values for x
.Remember, when working with cube roots, negative values under the cube root symbol are acceptable.
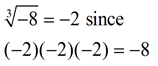 |

|
Negation of the parent function:, 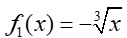 .
Properties:
• zero, domain, range, x-intercept, y-intercept, relative max/min, and absolute max/min remain the same.
• graph is decreasing from left to right across the domain.
The end behavior of this cube root function:
as x → -∞, f (x)
→ +∞
as x → +∞, f (x)
→ -∞,
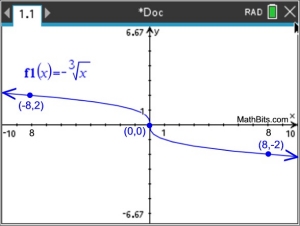
This negation graph is a reflection of the parent function over the x-axis. |
Negation of Cube Root Function
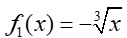
| x |
0 |
1 |
4 |
9 |
16 |
| f1(x) |
0 |
-1 |
-2 |
-3 |
-4 |
|

As additional root functions are examined, a pattern is noticeable.
All even root functions (2nd root, 4th root, 6th root, etc.), follow the pattern established by the square root function of having a terminating endpoint.
All odd root functions (3rd root, 5th root, 7th toot, etc) follow the pattern established by the cube root function of extending indefinitely in both directions.
Fourth Root Function 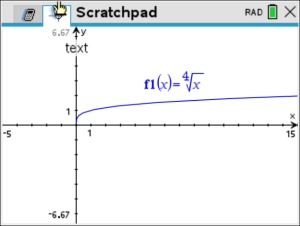 |
Fifth Root Function 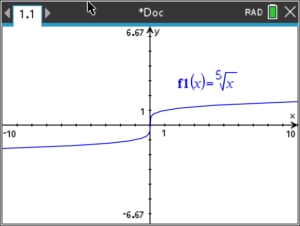 |

|
For
calculator help with graphing
radical functions.
click here. |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|

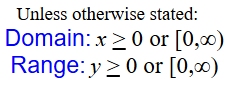



 |
|