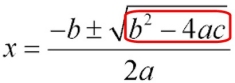When solving a quadratic equation, we are searching for the two solutions that will make the equation true. We have encountered situations where there appeared to be only one solution (a repeated root). And, we have encountered situations where there was no Real number solution to the equation (an imaginary/complex solution).

button Fortunately, there is a quick way to determine
an equation's "number and type of solutions".

The Quadratic Formula to the rescue again!


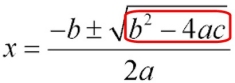
The discriminant is the portion "under" the square root symbol
in the Quadratic Formula:
The value under the square root symbol (the radicand) portion of the quadratic formula indicates the "number and type of solutions" for a specific quadratic equation.
That value is "b2 - 4ac".

b2 - 4ac is called the discriminant.

Note: The discriminant, b2 - 4ac, does NOT tell you what the solution(s) to the
quadratic equation will be. It simply tells you "the number and type" of solutions there will be.

Consider the equation ax2 + bx + c = 0.

If b2 - 4ac > 0, then the equation has two real solutions.

If b2 - 4ac = 0, then the equation has one real solution (repeated).

If b2 - 4ac < 0, then the equation has two imaginary solutions.


DISCRIMINANT: Its purpose is to tell "how many roots", and "what type of roots".
POSITIVE
b2 - 4ac > 0
ZERO
b2 - 4ac = 0
NEGATIVE
b2 - 4ac < 0
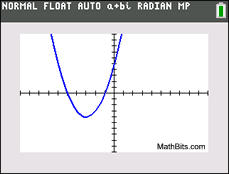
x2 + 6x + 5 = 0
discriminant:
b2 - 4ac = 62 - 4(1)(5)
= 16 (positive)
There are two real roots.
There are two x-intercepts.
graphn1
If the discriminant is a perfect square, the two roots are rational numbers. If the discriminant is not a perfect square, the two roots are irrational numbers containing a radical.
x2 + 6x + 5 = (x + 1)(x + 5) = 0
Roots: x = -1, x = -5
x2 - 2x+ 1 = 0
discriminant:
b2 - 4ac = (-2)2-4(1)(1)
= 0 (zero)
There is one real root.
There is one x-intercept.
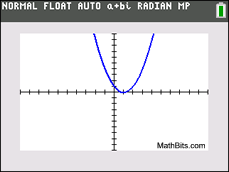
graphn2
(The root is repeated.)

x2 - 2x+ 1 = (x - 1)2
= (x - 1)(x - 1) = 0
Repeated root: x = 1

x2 - 3x + 10 = 0
discriminant:
b2 - 4ac = (-3)2-4(1)(10)
= -31 (negative)
There are 2 imaginary roots.
There are no x-intercepts.
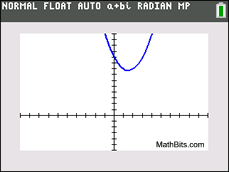graphn3
In this situation, there will be two "complex" (a + bi form) roots because there will be a negative number under the square root. Answers have imaginary number, i.

 

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".