|
Directions: Answer these questions using quadratic equations or functions. Check your answer when finished. You will need a calculator.
1. |
Thad is 3 years older than his brother Kevin. If the product of their ages is 180, how old are the brothers?
|
|
|
2. |
Hikers Angela and Tyler start out at the same point. Angela walks due north for x miles. In the same amount of time, Tyler, going due east, walks one mile further than Angela walked. When they stop, the distance between the hikers is 2 miles more than the distance walked by Angela. How far did each hiker walk? |
|
|
3.
|
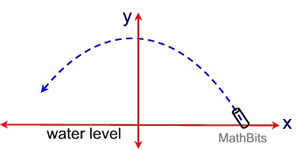
The path followed by one of the water spouts in a fountain can be modeled by the equation: 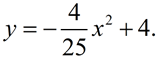 ("y" is measured in feet.)
("y" is measured in feet.) |
 |
|
a) Find the highest point reached on the water's arc, in feet above the water (pond) level.
b) Find the horizontal distance reached by the water's arc (that is, the distance from the bottom of the angled water spout to where the water's arc hits the pond).
c) If the water's arc leaves the angled spout 6 inches above the pond level, at what horizontal distance will the water's path again be at this 6 inch height above the pond? (To nearest tenth of a foot.)
|
|
|
4.
|
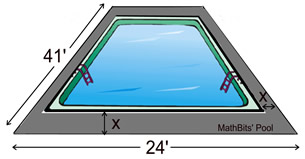
A new rectangular in-ground swimming pool is installed with a concrete sidewalk around the pool with a consistent width of x feet. The outside edge of the sidewalk measures 24 feet by 41 feet. If the area of the pool is 630 square feet, find the width of the sidewalk.
|
|
|
|
|
5.
|
A parabolic trough is a form of solar thermal collector which is curved as a parabola and lined with polished metal mirrors. The sun's rays enter the mirrors and are reflected to the focal line where objects to be heated are located. |
|
For this problem, the axis of symmetry of the parabolic trough will be represented by the y-axis with the vertex at (0,0). The focus is 6 feet from the vertex at point (0,6).
a) Find a parabolic equation that can be used to represent this trough.
b) A line through the focus, parallel to the x-axis, intersects the top and bottom edges of the trough at points A and B. Find the coordinates of points A and B.
c) Find AB.
|
|
|
6.
|
The area of a square is "4a" square inches. The perimeter of the square is "2a" inches. Find the number of inches in the length of a side of the square.
|
|
|
|
7.
|
Pumpkin chunking is the sport of hurling a pumpkin by means of a mechanical device such as a catapult. When hurled, the pumpkin follows a parabolic path until it smashes on the ground. A contestant's first meager attempt at hurling was modeled by the equation
y = -0.625x2 + 4.375x + 5 , where x was the horizontal distance traveled in feet, and y was the height of the pumpkin in feet.
|
|
a) At what height did the pumpkin leave the catapult?
(Assume all measurements begin when the pumpkin leaves the catapult.)
b) What was the total horizontal distance traveled by the pumpkin?
c) What was the maximum height reached by the pumpkin?
In each section, if needed, express answers to the nearest hundredth of a foot. |
|
|
8.
|
If you invest money, P, at an interest rate, r, compounded annually, then at the end of two years the amount, A, of money you will have is given by A = P(1 + r)2. At what rate will $100 increase to $144 in 2 years?
|
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|