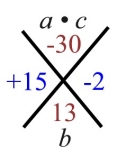|
Solving a Quadratic Equation: ax2 + bx +c = 0
Before continuing, see "Preview of Factoring by Grouping".
Factoring by Grouping for Polynomials of higher degrees will be discussed in Polynomials.
Before we move to solving quadratic equations, ax2 + bx +c = 0,
let's examine this process as it applies to factoring a quadratic expression, ax2 + bx +c. |
Note: this method will not apply to a quadratic equation with complex roots, as the numbers involved in this method
must be factors of the product of 2 real numbers, ac, while a complex quadratic involves the imarinary i.
Method: "Split the MIddle" or
"ac" Method & Factor by Grouping - Quadratics |
Notice, when we multiply (x + 4)(x + 6) we get x2+ 4x + 6x + 24 which equals x2 + 10x + 24.
Whenever you multiply two binomials, you create two "middle" terms, which in many cases are "like" terms and are then combined into one term. It is the creation of these two "middle" terms which becomes the focus of the "Split the Middle" or "ac" Method for factoring trinomials.
Keep in mind that we are working with quadratic expressions of the form ax2 + bx + c.
We know that with a leading coefficinet of 1,
the coefficients of those two middle terms (4x and 6x) must Add to 10,
and Multiply to 24. We will be searching for numbers that obey these patterns.
This method of creating two "middle" terms is called "split the middle" because it endeavors to create those two "middle terms" which will make the factoring process easier.
Once the middle is "split" into two parts, the process of "factoring by grouping" is used to arrive at the roots.
Since the method we will be using starts by dealing with the leading coefficient, a,
and the constant term, c, in the quadratic expression ax2 + bx + c,
this method is also referred to as the "ac" method of factoring quadratics.
 The "ac" Method of Factoring Quadratics - "Split the Middle":
Factor a trinomial of the form
ax2 + bx + c
|
Factor: 8x2 + 26x + 15 |
1. Always check for any common factors before you begin. |
There are no common factors in this quadratic. |
2. Find a • c (referred to as the Master Product).
If the leading coefficient is 1, you will simply be finding "c".
|
a • c = 8 • 15
= 120 |
3. Find two new numeric factors of a • c (120) that
will also add up to b (which is +26).
Factors of 120 are: 2•60. 3•40. 4•30. 5•24, 6•20. Stop!
For this problem, these two new numeric factors will be
20 and 6.
These values of 20 and 6 will become the coefficients of the two new middle terms of the trinomial. |
Numeric factors of the value a • c,
20 • 6 = 120
that also add to b.
20 + 6 = 26
20 and 6 will now be coefficients of the 2 new middle terms |
4. Split the middle term into two terms whose coefficients are the new factors of 20 and 6.
Surprisingly, the order of the middle terms does not matter. They will give the correct answer in either order.
|
8x2 + 20x + 6x + 15
order of middle terms does not matter
Notice that this expression is equivalent to the original trinomial. |
5. "Factor by Grouping": Group the four terms to form two binomial pairs. Be careful of the signs. (See example below for dealing with grouping a negative middle term.) |
(8x2 + 20x) + (6x + 15) |
6. Factor each pair by finding the common factors. |
4x(2x + 5) + 3(2x + 5) |
7. Factor out the common (shared) binomial. |
(2x + 5)(4x + 3) |
| 8. DONE! |
ANSWER: (2x + 5)(4x + 3) |
In plain English:
To get "Split the Middle" started,
you need to find two numbers that multiply to a • c,
and also add to the value of b.
These two numbers will be used to form 2 new
"middle terms", which will allow for
"factoring by grouping" to arrive at the answer.
|
|
A set-up for "factoring by grouping" can be seen in the picture above: (x2 + 3x) + (5x + 15).
To factor, we would normally need to combine the terms, and then factor the trinomial.
But "factoring by grouping" will be easier:
x(x + 3) + 5(x + 3) factor out the common factor from each binomial
(x + 3)•(x + 5) use Distributive Property in reverse to factor out the shared binomial (x + 3)
DONE!!!
 |
"Split the Middle" Method for Factoring Trinomials ("ac" Method)
This "short cut" method gets the "Good Math Keeping" seal of approval. The steps in this process make rational mathematical sense, and the original expression is visibly maintained throughout the solution. |
|
Visual Planner (using the Diamond Method): 
|
 |
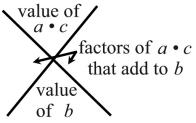| You may see a "visual planner" diagram, in the form of a large X, used to organize the numerical values in this "ac" Method of factoring. The two factors in the left and right corners of the X will be the coefficients of the two new "middle terms". |
Let's apply this visual planner to our previous example:
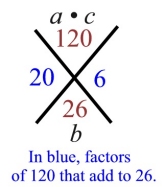
Factor: 8x2 + 26x + 15
In the top of the X, place the product of a = +8 and c = +15.
[8 • 15 = 120]
In the bottom of the X, place the value of b = +26.
Find the factors of 120 that will add up to 26, and place them in the right and left sections of the X.
Possible factors of 120 are:
2 • 60
3 • 40
4 • 30
5 • 24
6 • 20 Stop!
We found the pair that multiplies to 120 and adds to 26.
Insert the two middle terms, using 20 and 6 as coefficients.
Group the sections and factor to arrive at the answer.
8x2+ 20x + 6x + 15
(8x2 + 20x) + (6x + 15)
4x(2x + 5) + 3(2x + 5)
(2x + 5)(4x + 3) ANSWER
|
 |
Be careful when dealing with negative values in this "ac" Method.
1. Factor: 6x2 + 13x - 5 |
a • c = 6 • (-5) = -30 |
 |
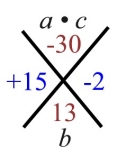(+15) • (-2) = -30
(+15) + (-2) = +13
These are the new factors that multiply
to a • c (-30) and add to b (+13). |
6x2 + 15x - 2x - 5 |
(6 x2 + 15x) - 1(2 x + 5)
 The safest way to "group" when the second middle term is negative is to factor out a "-1" from the second pairing. Less errors are made with this approach. |
3x(2x + 5) -1(2x + 5)
|
(2x + 5)(3x - 1) Answer |
2. Factor: 2x2 - 13x + 21
|
a • c = 2 • 21 = 42 |
 |
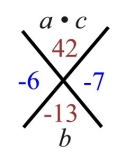(-6) • (-7) = 42
(-6) + (-7) = -13
These are the new factors that multiply
to a • c (42) and add to b (-13). |
2x2 - 6x - 7x + 21 |
(2x2- 6x) - 1(7x - 21)
Again, the safest way to "group" when the second middle term is negative is to factor out a "-1" from the second pairing. Less errors are made with this approach. |
2x(x - 3) - 1•7(x - 3)
2x(x - 3) - 7(x - 3) |
(x - 3)(2x - 7) Answer |
|
Solve quadratic equation using
"ac" method
& factor by grouping. |
3. Solve equation: 8x2 + 26x + 15 = 0 |
Find the factors of a • c that will add to b.
a = 8, b = 26, c = 15
8x2 + 20x + 6x + 15 = 0
a • c = 8 • 15
= 120
20 • 6 = 120 (factors of 120 that add to 26)
20 + 6 = 26
8x2 + 20x + 6x + 15 = 0 (create equivalent middle term)
(8x2 + 20x) + (6x + 15) = 0 (group)
4x(2x + 5) + 3(2x + 5) = 0 (factor by grouping)
(2x + 5)(4x + 3) = 0
2x + 5 = 0 4x + 3 = 0
2x = -5
4x = -3
x - -5/2
x = -3/4
|
Mathematically speaking, why does this "short cut" method work?
The reason this method of creating two new "middle terms" works, is due to the relationships between the terms and their coefficients when two binomials are multiplied together.
Consider: (mx + n) • (px + q)
m, n, p, q are constants (numbers)
x is the variable
mpx2 +mqx + npx + nq
notice the two middle terms as a result of distribution
mpx2 +(mq + np)x + nq
factor out x from the two middle terms
The factored coefficient of the middle term is (mq + np).
The product of the coefficient of the first term and the constant is mp • nq.
NOTE: mp • nq is the product of numbers, so we can rearrange the order (or mq • np).
mq is a factor of mq • np
np is a factor of mq • np
The product of these two factors is mq • np
The terms that create the sum for the middle term (mq and np) are factors of the product of the coefficient of the first term and the constant (mq • np).
(mpx2 +mqx) + (npx + nq)
split the middle, and group
mx(px + q) + n(px + q)
factor by grouping
(mx + n) • (px + q)
distributive property in reverse
The results from factoring by grouping return to us that with which we started.
|
For
calculator help with solve
quadratic
equations 1.
click here. |
|
|
|
For
calculator help
with solve
quadratic
equations 2
click here. |
|
|
|
For calculator help with solve
quadratic
equations
click here. |
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
