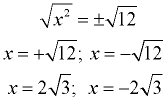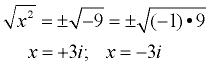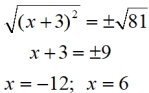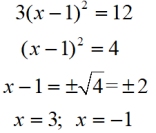|
Solving a Quadratic Equation: ax2 + bx +c = 0
| Method: Taking Square Roots |
 To solve a quadratic equation by taking a square root:
| |
Square
Root Method (ax2 is the only variable term) |
1. |
Isolate the ax2 term on one side of the equation. |
2. |
Take the square root of both sides. |
3. |
Remember to use ±, as there are two solutions. |
4. |
Express the roots (or zeros of the function). |
|
The square root method applies only to one specific situation. This method works when there is no middle bx-term in the equation. The only variable in the equation is an x2-term.
|
Examples of Solving Quadratic Equations by Square Root Method:
Easiest Set-Up (has "x2 = __"): |
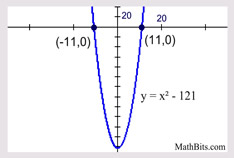
Solve: x2 = 121
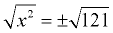
x = ±11
|
|
The square root method is actually an application of the inverse relationship between squaring and square rooting. Square rooting the square of a value will remove the square, leaving only the value. |
Difference of Two Squares:
|
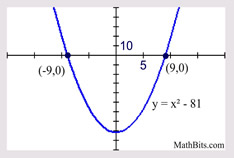
Solve: x2 - 81 = 0
x2 = 81
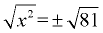
x = ± 9
|
|
While this is the difference of two squares, we can simply add 81 to both sides and we are back to the solution shown in the box above.
Yes, this can also be factored.
(x - 9)(x + 9) - 0 |
Only variable is the x2 term, with subtraction of constant. |
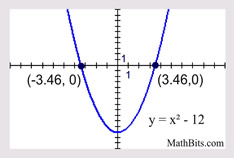
Solve: x2 - 12 = 0
x2 = 12
|
|
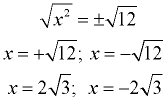
This example shows the numeric value (the constant), subtracted from the x2 term.
Approximate decimal answers:
x = -3.464102 and
x = 3.4641016 |
Only variable is the x2 term, with addition of constant. |
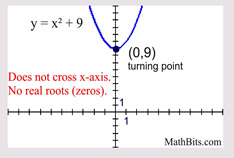
Solve: x2 + 9 = 0
x2 = -9
|
|
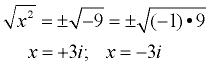
This example shows the numeric value (the constant), added to the x2 term, which creates "complex" answers containing the imaginary "i". |
Parentheses squared for an expression containing x. |
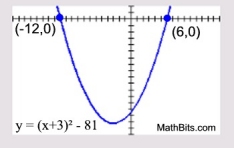
Solve: (x+3)2 = 81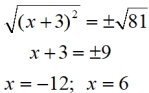 
|
|
This example shows x contained within a set of parentheses squared. Tale the square root of both sides. |
Parenthees, squared, coefficient, and additional terms surrounding expression of x. |
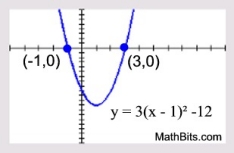
Solve: 3(x - 1)2 - 2 = 10
|
|
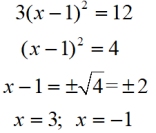
This example shows isolating the squared parentheses, then taking the square root of both sides. |
There are tools more powerful than the square root method for solving quadratic equations.
Return to the Topic Outline for other solution methods.
|
For
calculator help with solve
quadratic
equations 1.
click here. |
|
|
|
For
calculator help
with solve
quadratic
equations 2
click here. |
|
|
|
For calculator help with solve
quadratic
equations
click here. |
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
