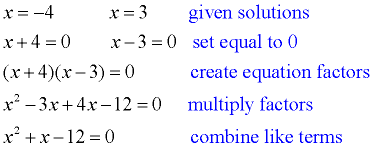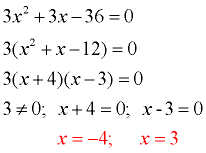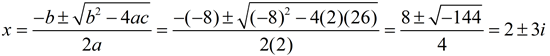|
 Can you determine the equation of a quadratic given its solutions?
If you are given the solutions of an equation, you can find an equation by working backward.
Let's see what happens when we use this strategy.
1. a. Determine an equation that has the solutions x = -4 and x = 3.
Work backward to find the equation: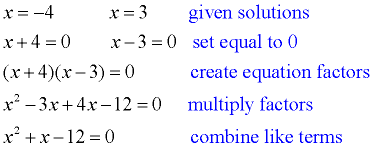
We now have an equation answer:
x2 + x - 12 = 0 |
1. b. Find the solutions for the equation 3x2 + 3x - 36 = 0.
This equation can be solved by factoring.
|
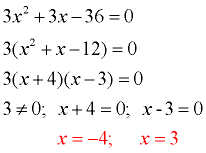
WHOA! We have two different quadratic equations with the same solution.
|
Conclusion:
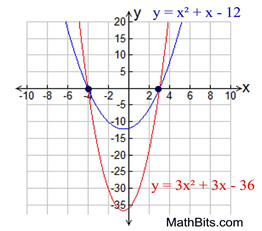
Working backward will create an equation, but remember that there are other equations that will also have that same set of solutions.
(Compare the solutions in 1a with 1b, and take a look at the graph at the right.)
Any equation of the form k(x2 + x - 12) = 0, where k is a constant, has the same solutions as
x2 + x - 12 = 0.
|
 |
|
Yes, you can determine the equation of a quadratic given its solutions, BUT the
solution will not be unique (there will be more than one possible equation).
|
NOTE: If a quadratic equation is multiplied by a constant (a number), the new quadratic will have the same roots as the original, but their graphs will be different. |
Can we use this same strategy with complex solutions?
2. a. Determine an equation that has the solutions x = 2 + 3i and x = 2 - 3i.
Work backward to find the equation:
An equation that has these roots is
x2 - 4x + 13 = 0
|
2. b. Does the equation 2x2 - 8x + 26 = 0 have these same roots? YES!!
 |
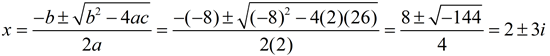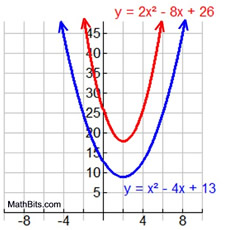
Conclusion:
As we saw in example 1, there are other equations that will also have that same set of solutions.
(Compare the solutions in 2a with 2b.)
Unlike example 1, however, it is not obvious from looking at the graphs of these equations that their roots are the same, since they do not cross the x-axis.
Again, we see that any equation of the form
k(x2 - 4x + 13) = 0, where k is a constant, has the same complex roots as
x2 - 4x - 13 = 0.
|
 |
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
