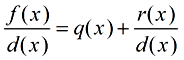When working with Synthetic Division, we saw a series of division problems involving a divisor of the
form (x - a), called a linear factor since the degree of the divisor was one. When you divide a polynomial by a a linear factor
such as (x - a), the remainder will have a degree of 0. Thus, the remainder will be a constant, such as "2").
Before we continue, consider:
Division Algorithm for Polynomials
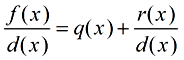 |
|
If we multiply each side of the Division Algorithm
by the divisor, d( x), we have: 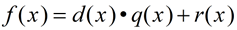 |
f (x) is the polynomial or dividend; d(x) is the divisor; q(x) is the quotient; r(x) is the remainder
Now, if we use this new equation when working with a divisor of (x - a), we have:
f (x) = (x - a) • q(x) + r(x)
But, r(x) is simply a constant, since we are dividing by a degree of 1, so replace r(x) with just r:
f (x) = (x - a) • q(x) + r
Now, when x = a, we have:
f (a) = (a - a) • q(a) + r
f (a) = (0) • q(a) + r
f (a) = r
We now have the basis of the Remainder Theorem for Polynomials:
 |
The Polynomial Remainder Theorem: When the polynomial f (x) is divided by a linear factor, such as (x - a), the remainder equals f (a). |
|
 |
This is a Great discovery!!
Now, when you divide a polynomial, f (x), by (x - a), you won't need to actually do the division to find the remainder. Simply calculate f (a). Plug a into f (x) and the answer is the remainder. |
 The most valuable use of this discovery is to determine if the divisor (x - a) is a factor of the dividend. If (x - a) is a factor of f (x), the remainder will be zero. You can quickly make this determination by plugging a into f (x) to see if the result is zero.
The most valuable use of this discovery is to determine if the divisor (x - a) is a factor of the dividend. If (x - a) is a factor of f (x), the remainder will be zero. You can quickly make this determination by plugging a into f (x) to see if the result is zero.
A special case of the Remainder Theorem, used to determine a factor, is called
the Factor Theorem. We saw this theorem at work in Algebra 1.
 |
The Factor Theorem: If f (a) = 0 for polynomial f (x), then (x - a) must be a factor of the polynomial. |
Converse: |
If (x - a) is a factor of polynomial f (x), then f (a) = 0. |
|
The factor theorem links factors and roots (zeros) of a polynomial.
factor (x - 2); f (2) = 0; 2 is a zero (root) of f (x)

Let's take a look at some example questions:
 Find the remainder when 4x2 + 2x - 5 is divided by (x - 1). Find the remainder when 4x2 + 2x - 5 is divided by (x - 1). |
Using the Remainder Theorem, we can find this answer quickly.
Think of f ( x) = 4 x2 + 2 x - 5 and solve for f (1). Notice that we are substituting "1", the root value associated with ( x - 1).
f (1) = 4(1)2 + 2(1) - 5 = 1 The remainder is 1. |

 Is (x + 4) a factor of x4 + 6x3 + 7x2 - 6x - 8? Is (x + 4) a factor of x4 + 6x3 + 7x2 - 6x - 8? |
Remember that when a polynomial is divided by a "factor", the remainder is zero. We simply need to use the Remainder Theorem (or its special case, the Factor Theorem) to see if the remainder is zero.
f (-4) = (-4)4 + 6(-4)3 +7(-4)2 - 6(-4) - 8
= 256+ (-384) + 112 - (-24) - 8 = 0
The remainder is 0, so (x + 4) is a factor.
|

 |
Given P(x) = x3 + 3x2 + ax - 15.
Find a if (x - 3) is a factor of P(x). |
|
If ( x - 3) is a factor of P( x), then P(3) will be zero. Set P(3) = 0 and solve for a.
P(3) = 33 + 3(3)2 + a(3) - 15
0 = 33 + 3(3)2 + a(3) - 15
0 = 27 + 27 + 3a - 15
0 = 39 + 3a
-39 = 3a
-13 = a
If (x - 3) is a factor of P(x), then a = -13.
|