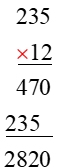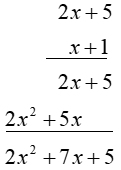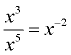|
 Polynomials form a system similar to the system of integers.
A polynomial system's structure is composed of expressions containing variables and exponents.
An integer system's
structure is composed of whole numbers that are positive, negative and zero.
While these two systems have differing "structures", they have certain attributes in common.
You may see the expression, "polynomials and integers are analogous systems."
The word "analogous" simply means "a comparison of similarities".
| "Observable" Similarities between Polynomials and Integers: |
Under the decimal number system, (base 10 system), we know that every value
in this system
is based upon the number 10.
Consider the number 4,372.
4000 + 300 + 70 + 2 = 4372
4 x 1000 + 3 x 100 + 7 x 10 + 2 x 1 = 4372
4 • 10³ + 3 • 10² + 7 • 10¹ + 2 • 10° = 4372 |
The place values within a number represent a connection to powers of 10.
But ... what if we did NOT know that this number was base 10?
Since we commonly deal with unknowns in Algebra by using "x",
let's replace the base value with an "x":
4 • 103 + 3 • 102 + 7 • 101 + 2 • 100
4 • x3 + 3 • x2 + 7 • x1 + 2 • x0
We just created a polynomial-type value: 4x3 + 3x2 + 7x + 2.
Polynomials may be thought of as representing values in base "x".
Please Note: This discussion compares polynomials to the system of integers (not Real numbers).
When working with number bases, it is possible to represent "decimals" within the base being discussed.
For example, in base 10, the number 12.5 = 1 x 101 + 2 x 100 + 5 x 10-1
This idea of representing "decimals" does not apply to polynomials in base "x", since polynomials do not allow the base value to be raised to a negative exponent. Thus, the polynomial comparison is to the system of integers only.

|
| Similarities in "Properties of Operations" |
The Distributive Property:
| Integers |
Polynomials: |
| 2(6 + 4) = 2 • 6 + 2 • 4 = 12 + 8 = 20 |
2x(x + 7) = 2x • x + 2x • 7 = 2x2 + 14x |
Multiplication:
| Integers |
Think about how these two multiplication examples are similar.
• Both examples start the process with the right digit in the second row, and multiply the first row.
• Move to the left digit in the second row, and multiply the first row.
• The results, as obtained, are lined up in a similar manner.
•
The columns are totaled for the final answers. |
Polynomials: |
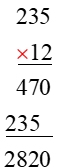 |
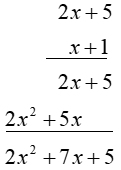 |
Division:
| Integers |
Polynomials: |
 |
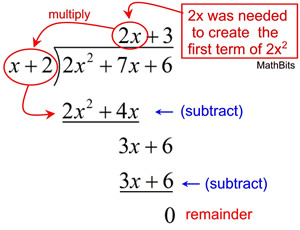 |
| These two division examples show basically the same set up and the same process at work. |

| Similarities in "Mathematical" Properties: |
The polynomial system and the integer system are analogous in that:
• both systems are closed under addition, subtraction and multiplication. (Closure)
• both systems have a unique prime factorization. (The Fundamental Theorem of Arithmetic)
CLOSURE: Both the polynomial system and the integer system are "closed" under the operations of addition, subtraction, and multiplication. Closure means that when you perform one of these operations on the values in the system, the result will always be another value within the same system. |
Note: Polynomials are not closed under DIVISION.
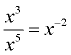 |
When dividing variables with exponents, there is the possibility of creating a negative exponent. Negative exponents are not allowed in polynomials. |
UNIQUE PRIME FACTORIZATION: Both the polynomial system and the integer system have a unique prime factorization.
Integers: This is the property that every integer (greater than one) can be broken down into a product of prime numbers in only one way, ignoring the order of the factors.
Example: 20 = 2 x 2 x 5
Polynomials: This is the property that every polynomial (non-zero) can be written as a product of a finite number of irreducible polynomials in a unique way, ignoring the order and the units. (This is like factoring a polynomial into its prime factors.)
Example: x3 + 2x2 - x - 2 = (x - 1)(x + 1)(x + 2)
The Fundamental Theorem of Arithmetic states that every integer greater than 1 is either a prime number itself or can be written as a unique product of prime numbers, regardless of the order of the factors. |

FYI: While we know and love base 10 values, there are other number bases at work around us. Base 2 (binary number system) and base 16 (hexadecimal number system) are frequently used in computer science and technology. Even the numbers used to specify the colors you see on this HTML web page use a hexadecimal system ("000000" is black and "ffffff" is white). Yes, there are letters in the hexadecimal system.
(For more information about working with number bases, view:
number bases; converting from base 10; converting to base 10; converting via base 10.)

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|