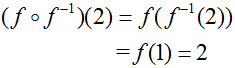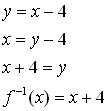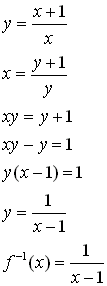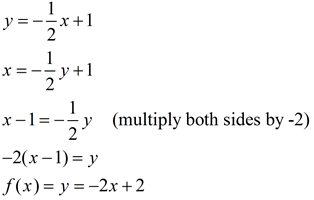|
Inverse functions were examined in Algebra 1. See the Refresher Section to revisit those skills.
A function and its inverse function can be described as the "DO" and the "UNDO" functions. A function takes a starting value, performs some operation on this value, and creates an output answer. The inverse function takes the output answer, performs some operation on it, and arrives back at the original function's starting value. This "DO" and "UNDO" process can be stated as a composition of functions.
A function composed with its inverse function yields the original starting value.
Think of them as "undoing" one another and leaving you right where you started.
If functions f and g are inverse functions, 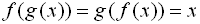 . |
Basically speaking, the process of finding an inverse is simply the swapping of the x and y coordinates. This newly formed inverse will be a relation, but may not necessarily be a function.
 |
 The inverse of a function may not always be a function!
The original function must be a one-to-one function to guarantee that its inverse will also be a function.
|
 |
A function is a one-to-one function if and only if each second element corresponds to one and only one first element. (Each x and y value is used only once.) |
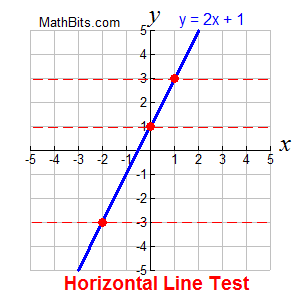
Use the horizontal line test to determine if a function is a one-to-one function.
If ANY horizontal line intersects your original function in ONLY ONE location, your function will be a one-to-one function and its inverse will also be a function.
The function y = 2x + 1, shown at the right, IS a one-to-one function and its inverse will also be a function.
(Remember that the vertical line test is used to show that a relation is a function.) |
 |
|
An inverse relation is the set of ordered pairs obtained by interchanging the first and second elements of each pair in the original function.
|
If the graph of a function contains a point (a, b), then the graph of the inverse relation of this function contains the point (b, a).
Should the inverse relation of a function f (x) also be a function,
this inverse function is denoted by f -1(x).
Note: If the original function is a one-to-one function, the inverse will be a function.
|
|
If a function is composed with its inverse function,
the result is the starting value. Think of it as the function and the inverse undoing one another when composed.
Consider the simple function f ( x) = {(1,2), (3,4), (5,6)}
and its inverse f-1( x) = {(2,1), (4,3), (6,5)}
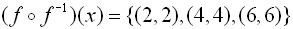 |
More specifically:
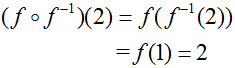 The answer is the starting value of 2.
The answer is the starting value of 2. |

Finding inverses: Let's refresh the 3 methods of finding an inverse.
Swap ordered pairs:
If your function is defined as a list of ordered pairs, simply swap the x and y values. Remember, the inverse relation will be a function only if the original function is one-to-one.
|
Example 1:
Given function f, find the inverse relation. Is the inverse relation also a function?
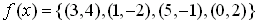
Answer:
Function f is a one-to-one function since the x and y values are used only once.
Since function f is a one-to-one function, the inverse relation is also a function.
Therefore, the inverse function is:
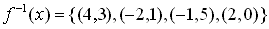
Example 2:
Determine the inverse of this function. Is the inverse also a function?
| x |
1 |
-2 |
-1 |
0 |
2 |
3 |
4 |
-3 |
| f (x) |
2 |
0 |
3 |
-1 |
1 |
-2 |
5 |
1 |
Answer: Swap the x and y variables to create the inverse relation. The inverse relation will be the set of ordered pairs:
{(2,1), (0,-2), (3,-1), (-1,0), (1,2), (-2,3), (5,4),(1,-3)}
Since function f was not a one-to-one function (the y value of 1 was used twice), the inverse relation will NOT be a function (because the x value of 1 now gets mapped to two separate y values which is not possible for functions).

Solve algebraically:
Solving for an inverse relation algebraically is a three step process:
|
|
1. Set the function = y
2. Swap the x and y variables
3. Solve for y |
|
Example 1:
Find the inverse of the function 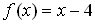
Answer:
|
Remember:
Set = y.
Swap the variables.
Solve for y.
You can use the inverse function notation since f (x) is a one-to-one function. |
Example 2:
Find the inverse of the function 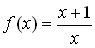 (given that x is not equal to 0). (given that x is not equal to 0).
Answer:
|
Remember:
Set = y.
Swap the variables.
Eliminate the fraction by multiplying each side by y.
Get the y's on one side of the equal sign by subtracting y from each side.
Isolate the y by factoring out the y.
Solve for y.
You can use the inverse function notation since f (x) is a one-to-one function. |
Example 3:
Given f -1(x) = -½ x + 1, express the equation of f (x).
Answer:
At first glance, this question may look like a completely different type of problem, but it is not. Apply the same strategy that was used in Example 1.
(f (x) is actually the inverse of f-1(x).)

Graph:
The graph of an inverse relation is the reflection of the original graph over the identity line,y = x.
It may be necessary to restrict the domain on certain functions to guarantee that the inverse relation is also a function.
|
Example 1:
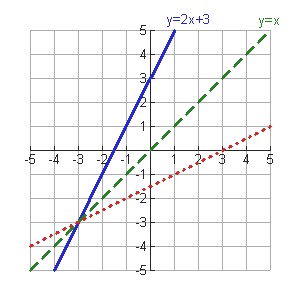
Graph the inverse of y = 2x + 3.
Consider the straight line, y = 2x + 3, as the original function. It is drawn in blue.
If reflected over the identity line, y = x, the original function becomes the red dotted graph. The new red graph is also a straight line and passes the vertical line test for functions. The inverse relation of y = 2x + 3 is also a function.
Not all graphs produce an inverse relation which is also a function. |
 |
Example 2:
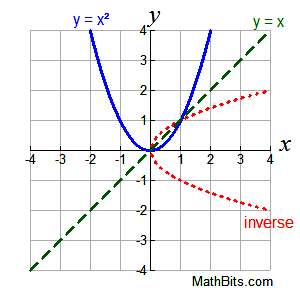 You can see that the inverse relation exists, but it is NOT a function. You can see that the inverse relation exists, but it is NOT a function. |
Sketch the graph of the inverse of y = x2. State whether the inverse is a function.
First, we get the inverse by reflecting the given function over the identity line y = x.
Then we look at the inverse to see if it is a function (does it pass the vertical line test for functions?), or is it simply a relation.
The example at the left shows the original function,
y = x2 , in blue. Its reflection over the identity line
y = x is shown in red is its inverse relation. The red dashed line will not pass the vertical line test for functions,
thus y = x2 does not have an inverse function - it has an inverse relation..
|

|
The graph of 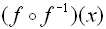 will equal x, the starting value.
The graph of a function composed with its inverse function is the identity line y = x.
|
|
For calculator help with
inverse of functions
click here. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|