1. |
Given the function f (x) = 5x + 4, find f (2m).
Solution: Substitute 2m into the function in place of x. f (2m) = 5(2m) + 4 = 10m + 4.
Using parentheses will avoid problems.
Notice that the answer is an algebraic expression, not a numeric value.
|
2. |
Given f (x) = 3x2 + 2x - 3, find f (2a - 5).
Solution: Parentheses are a MUST is this problem!
Be careful - more algebra work is needed here.
f (2a - 5) = 3(2a - 5)2 + 2(2a - 5) - 3
= 3(4a2 - 20a + 25) + 4a - 10 - 3
= 12a2 - 60a + 75 + 4a - 10 - 3
=
12a2 - 56a + 62
|
3. |
Given g ( a) = 9 - a2 and h ( a) = a - 3, express:
| a) g (a) + h (a) |
b) g (a) - h (a) |
| c) g (a) • h (a) |
d) 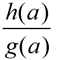 , g(a) ≠ 0 , g(a) ≠ 0 |
Solution:
a) g (a) + h (a) = (9 - a2) + (a - 3)
= -a2 + a + 6 |
b) g (a) - h (a) = (9 - a2) - (a - 3)
= -a2 - a + 12 |
c) g (a) • h (a) = (9 - a2) • (a - 3)
= -a3 + 3a2 + 9a - 27 |
d) 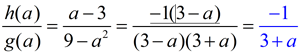
a ≠ 3; a ≠ -3 |
|
4. |
Given 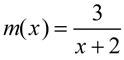 , express 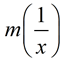 .
Solution: Warm up your algebraic fraction skills!
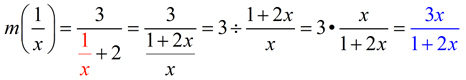
|
5. |
Given f (x) = x2 - x - 4. Find f (x + h).
Solution: Be careful to replace the x with (x + h). Use parentheses!!!!
(x+h)2 - (x+h) - 4
x2 + 2xh + h2 - x - h - 4
|
|
|
6. |
Given g(x) = x2 + 1 and h(x) = 5 - x. Express 3•g(5 - x) - 2•h(x2)
Solution: Remember to use parentheses!
3g(5 - x) - 2h(x2) = 3((5 - x)2 + 1) - 2(5 - x2) = 3(x2 - 10x + 25 + 1) - 2(5 - x2)
= 3x2 - 30x + 78 - 10 + 2x2 = 5x2 - 30x + 68 |
7. |
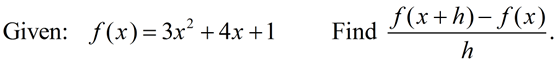
Solution: FYI: This new expression is called the "difference quotient" or average rate of change.
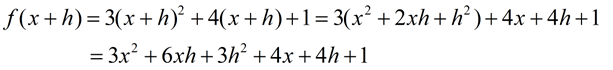
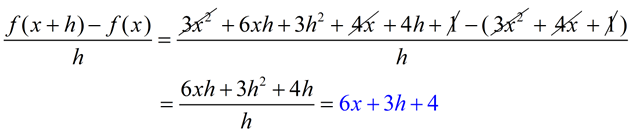
|