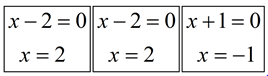|
Topics: Polynomial functions: continuous, turning points, roots, multiplicity, end behavior.
If looking for Functions: Intercepts, Positive/Negative, and Increasing/Decreasing, see Function Features.
If looking for Functions: Maximum/Minimum, Symmetry, End Behavior, see More Function Features.
|
A polynomial function is a function which is defined by a polynomial.
(In plain English, it's a polynomial expression set equal to f(x), or some other notation.)
Examples: f(x) = x2 + x - 6; P(x) = x3 - x2 - 12x; y1 = x2 + 4x + 4 |
Basic information about the graphs of polynomial functions:
1. Continuous: The graphs of polynomial functions are continuous. You can draw the entire function without lifting your pencil from your paper.
|
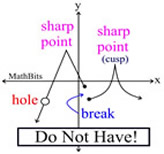
2. Smooth: The graphs of polynomial functions are always nice smooth graphs. The graphs do not contain holes, breaks or sharp point corners.
 |
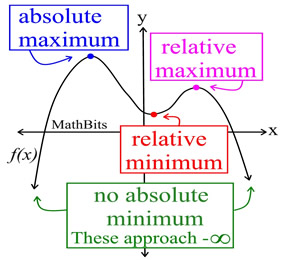
3. Turning Points: The "hills" or "valleys" where the graph changes direction from increasing to decreasing, or from decreasing to increasing, are often called turning points.
 The number of turning points is
never more than the degree of the
polynomial minus one.
|
For example, the graph of a 3rd degree polynomial function can have 2 turning points or fewer. If the degree is n, the number of turning points is at most n - 1. There could be fewer. |
|
Other terms for turning points can be relative maximum (or minimum) or local maximum (or minimum). The designation of "relative" (or "local") tells you that while this point may be a turning point, it may not be the maximum (or minimum) value reached by this function. It is only a maximum (or minimum) "relative" to a small section of the function surrounding this point. The one, true, largest (or smallest) value reached by the entire function is called the absolute maximum (or minimum), or the global maximum (or minimum).
FYI: The plural of maximum is maxima. The plural of minimum is minima. Discussions of maxima and minima are referred to as extrema. |
|
The connection between factoring and graphing polynomial functions:
4. Real Roots (or Zeros):
 |
If you plug in r (some real number) for x in a polynomial function, P(x), and get an answer of 0, the number, r, is called a root, or zero, of the polynomial. |
It can be quite tedious to repeatedly test random numbers looking for those numbers that give an answer of zero. A faster method for finding these roots (or zeros), is to factor the polynomial, and then set the factors equal to zero (the desired answer).
This factoring method for finding roots, or zeros, utilizes the zero factor principle which states that "if a • b = 0, then either a = 0 and/or b = 0."
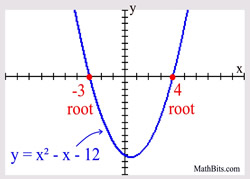
The real numbers that create the roots (or zeros) of a polynomial correspond to the x-intercepts of the graph of the polynomial function. |
This is valuable information when it comes to creating the graph of a polynomial (without a graphing calculator). It is also valuable if you are given the graph and are attempting to create a possible equation.
Note: A polynomial of degree 2 will have two roots (zeros), a polynomial of degree 3 will have three roots (zeros), and so on.
|
|
Example:
|
What happens to the graph when a factor repeats?
5. Multiplicity of Roots (or Zeros):
We have seen in the section above that the roots (zeros) of a polynomial correspond with the x-intercepts of the polynomial graph. In some situations, the graph will "cross" the x-axis at these points. In other situations, the graph may simply "touch" (be tangent to) the x-axis at these points. Let's see if we can determine, before we draw the graph, whether it will "cross" the x-axis at each root, or simply "touch" (be tangent to) the x-axis at each root.
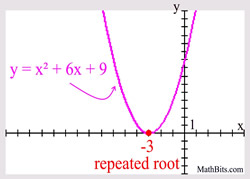
Consider the example at the right. The polynomial is of degree two, so there will be two roots (zeros). The factor of (x + 3) is repeated twice, and can also be written as (x + 3)2.
|
The number of times a factor appears in a polynomial is referred to as its multiplicity. |
In the example at the right, the factor (x + 3) has a multiplicity of 2, since it appears twice. It creates a "repeated root".
Multiplicity EVEN: When the multiplicity (the number of times a factor repeats) is two (or even), the graph will just "touch" (be tangent to) the x-axis at that point. |
Why? "EVEN" multiplicities are factors that occur an even number of times (2, 4, 6, ...), and form squares. Since squares are always positive, the graph near the root (zero) will not change signs from positive (above the x-axis) to negative (below the x-axis), or vice versa. The graph will "touch" the x-axis at the root (zero) but remain on the same side of the x-axis.
|
Example degree 2:
|
What if the multiplicity is ODD?
Consider the example at the right. The polynomial is of degree three, so there will be three roots (zeros). The factor (x - 2) appears twice and the factor (x + 1) once. (x - 2)2(x + 1) - 0
Multiplicity ODD: When the multiplicity (the number of times a factor repeats) is one (or odd), the graph will "cross" the x-axis at that point. |
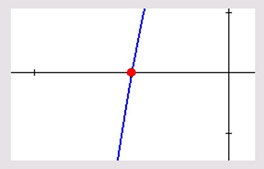
It is important to note that the single "crossing" point in this graph is from a "linear" factor. (A linear factor (x + 1)1 has a power of 1.)
If we ZOOM in on the root x = 1, we can see that the graph has a "linear" appearance as it crosses the x-axis close to the root. The graph looks like a straight line as it crosses the x-axis.
|
Example degree 3:
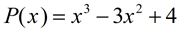
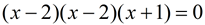
Set each factor = 0.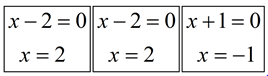
Roots: x = 2 (repeated), x = 1
|
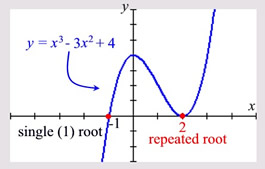
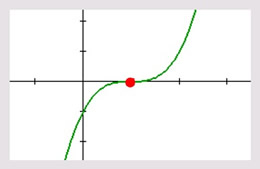
Another detail about ODD multiplicity.
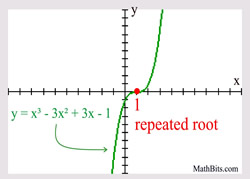
Consider the example at the right. The polynomial is of degree three, so there will be three roots (zeros). The factor of (x - 1) appears three times, and can be written as (x - 1)3.
Multiplicity ODD: When the multiplicity (the number of times a factor repeats) is three or more (and odd), the graph will show a flexing and flattening as it "crosses" the x-axis at that point. |
In the last example, we saw that the "crossing" of the x-axis had the appearance of a straight line surrounding the crossing. That occurred because a power of 1 yields a linear factor. What happens when the odd multiplicity is > 1 ?
If we ZOOM in on the root x = 1 from the graph at the right, we can see that the graph does NOT give the appearance of straight line as it crosses the x-axis.
Instead, the graph appears to flatten out as it crosses the x-axis. This flexing and flattening around the point (1,0) tells us that the multiplicity of x = 1 must be greater than 1. From the equation, we know this multiplicity is 3.
 |
|
Did you notice?
If you see a factor such as (x - 1)3, the multiplicity is 3.
If you see a factor such as (x + 2)2, the multiplicity is 2.
If you see a factor such as (x + 3)1, the multiplicity is 1. |
Note: When you factor a polynomial, the sum of the multiplicities equals the degree of the polynomial.
x3 + x2 - 5x + 3 =
(x - 1)2(x + 3) = (x - 1)2(x + 3)1
degree = 3
sum of multiplicities = 2 + 1 = 3
|
|
The end behavior of polynomial functions:
6. End Behavior: Examining the DEGREE of the polynomial and the SIGN of the leading coefficient will indicate what is happening at the ends of a polynomial function graph. Remember that end behavior refers to the appearance of a graph as it is followed indefinitely in either direction.
|
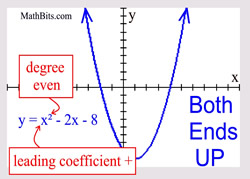
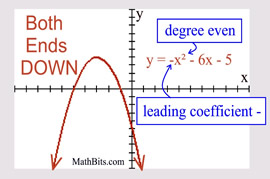
Even Degree Polynomial
("ends" behave similar to a quadratic) |
Leading coefficient POSITIVE: both "ends" are UP.
Leading coefficient NEGATIVE: both "ends" are DOWN.
|
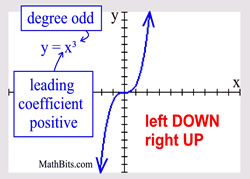
Odd Degree Polynomial
("ends" behave similar to a cubic) |
Leading coefficient POSITIVE: left end is DOWN and right end is UP.
Leading coefficient NEGATIVE: left end is UP and right end is DOWN.
|
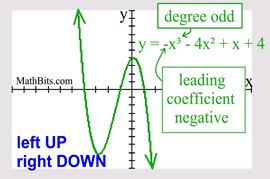
The graphing calculator can prove to be helpful for checking your answer when factoring and graphing. |
|
For help with factoring on your calculator,
Click Here!
|
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
